Как провести полное исследование функции

В данной статье рассмотрим схему исследования функции, а также приведем примеры исследования на экстремумы, монотонность, асимптоты данной функции.

Схема

1. Область существования (ОДЗ) функции.
2. Пересечение функции (если имеется) с осями координат, знаки функции, четность, периодичность.
3. Точки разрыва (их род). Непрерывность. Асимптоты вертикальные.
4. Монотонность и точки экстремума.
5. Точки перегиба. Выпуклость.
6. Исследование функции на бесконечности, на асимптоты: горизонтальные и наклонные.
7. Построение графика.

Исследование на монотонность

Теорема. Ежели функция g непрерывна на [a, b], дифференцированная на (а; b) и g’(x) ≥ 0 (g’(x)≤0), xє(а; b), то g возрастающая (убывающая) на [a, b].

Пример:

y = 1 : 3x³ – 6 : 2x² + 5x.

ОДЗ: хєR

y’ = x² + 6x + 5.

Найдем промежутки постоянных знаков y’. Поскольку y’ - элементарная функция, то она может менять знаки только в точках, где она превращается в ноль или не существует. Ее ОДЗ: хєR.

Найдем точки, производная в которых равняется 0 (нулю):

y’ = 0;

x = -1; -5.

Итак, y растущая на (-∞; -5] и на [-1; +∞), y нисходящая на [1; 2].

Исследование на экстремумы

Т. x₀ именуют точкой максимума (max) на множестве А функции g тогда, когда принимается в этой точке функцией значение наибольшее g(x₀) ≥ g(x), xєА.

Т. x₀ именуют точкой минимума (min) функции g на множестве А тогда, когда принимается в этой точке функцией значение наименьшее g(x₀) ≤ g(x), xєА.

На множестве А точки максимума (max) и минимума (min) именуются точками экстремума g. Такие экстремумы еще называют абсолютными экстремумами на множестве.

Если x₀ - экстремума точка функции g в некотором своем округе, то x₀ именуется точкой локального или местного экстремума (max или min) функции g.

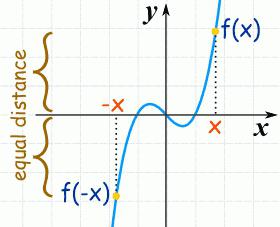
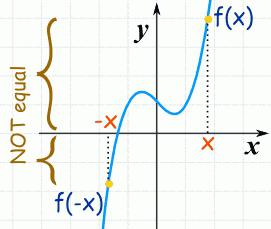
Теорема (условие необходимое). Если x₀ - точка экстремума (локального) функции g, то производная не существует или равна в этой т. 0 (нулю).

Определение. Критическими именуют точки с несуществующей или равной 0 (нулю) производной. Именно данные точки подозрительны на экстремум.

Теорема (условие достаточное № 1). Если функция g непрерывна в некотором округе т. x₀ и знак меняет чрез эту точку при переходе производная, то данная точка есть т. экстремума g.

Теорема (условие достаточное № 2). Пускай функция в некотором округе точки дифференцируема дважды и g’ = 0, а g’’ > 0 (g’’ < 0), тогда эта точка есть точкой максимума (max) или минимума (min) функции.

Исследование на выпуклость

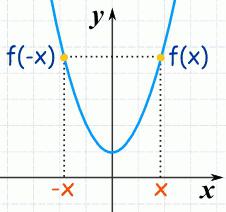
Функцию называют выпуклой вниз (или вогнутой) на интервале (а, b) тогда, когда график функции располагается не выше секущей на промежутке для любых x с (а, b), которая проходит чрез эти точки.

Функция будет выпуклой строго вниз на (а, b), если - график лежит ниже секущей на промежутке.

Функцию называют выпуклой вверх (выпуклой) на промежутке (а, b), если для любых точек с (а, b) график функции на промежутке лежит не ниже секущей, проходящей через абсциссы в этих точках.

Функция будет строго выпуклой вверх на (а, b), если - график на промежутке лежит выше секущей.

Если функция в некотором округе точки непрерывна и через т. x₀ при переходе функция изменяет выпуклость то эта точка именуется точкой перегиба функции.

Исследование на асимптоты

Определение. Прямую называют асимптотой g(x), если при бесконечном удалении от начала координат к ней приближается точка графика функции: d(M,l).

Асимптоты могут быть вертикальные, горизонтальные и наклонные.

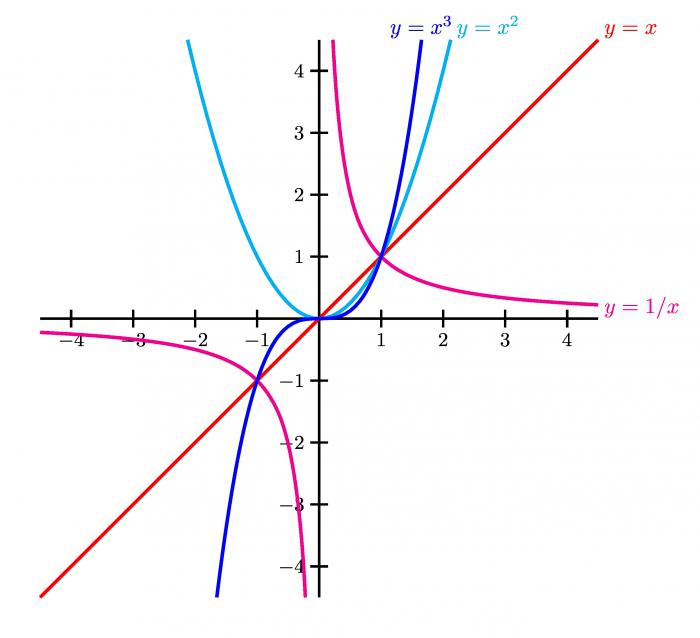
Вертикальная прямая с уравнением x = x₀ будет асимптотой вертикальной графика функции g, если в т. x₀ бесконечный разрыв, то есть хотя бы одна левая или правая граница в этой точке - бесконечность.

Исследование функции на отрезке на значение наименьшее и наибольшее

Если функция непрерывна на [a, b], то по теореме Вейерштрасса существует значение наибольшее и значение наименьшее на этом отрезке, то есть существуют точки, которые принадлежат [a, b] такие, что g(x₁) ≤ g(x) < g(x₂), x₂ є [a, b]. Из теорем про монотонность и экстремумы получаем следующую схему исследования функции на отрезке на наименьшее и наибольшее значение.

План

1. Найти производную g’(x).
2. Искать значение функции g в этих точках и на концах отрезка.
3. Найденные значения сравнить и выбрать наименьшее и наибольшее.

Замечание. Если нужно произвести исследование функции на конечном интервале (а, b), или на бесконечном (-∞; b); (-∞; +∞) на max и min значение, то в плане вместо значений функции на концах промежутка ищут соответствующие односторонние границы: вместо f(a) ищут f(a+) = limf(x), вместо f(b) ищут f(-b). Так можно найти ОДЗ функции на промежутке, потому что абсолютные экстремумы не обязательно существуют в данном случае.

Применение производной к решению прикладных задач на экстремум некоторых величин

1. Выражают данную величину через другие величины из условия задачи так, чтобы она была функцией только от одной переменной (если это возможно).
2. Определяют промежуток изменения этой переменной.
3. Проводят исследование функции на промежутке на max и min значения.

Задача. Нужно построить площадку прямоугольной формы, использовав а метров сетки, у стены так, чтобы с одной стороны она прилегала к стене, а с остальных трех была ограждена сеткой. При каком соотношении сторон площадь такой площадки будет наибольшей?

S = xy - функция 2 переменных.

S = x(a - 2x) - функция 1-й переменной; x є [0; a:2].

S = ax - 2x²; S' = a - 4x = 0, xєR, x = a : 4.

S(a : 4) = a² : 8 - наибольшее значение;

S(0) =0.

Найдем другую сторону прямоугольника: у = a : 2.

Соотношение сторон: y : x = 2.

Ответ. Наибольшая площадь будет равна a²/8, если сторона, которая параллельна стене, в 2 раза больше другой стороны.

Исследование функции. Примеры

Пример 1

Имеется y=x³ : (1-x)². Произвести исследование.

1. ОДЗ: хє(-∞; 1) U (1; ∞).
2. Общего вида функция (ни четная, ни нечетная), относительно точки 0 (нуль) не симметрична.
3. Знаки функции. Функция элементарная, поэтому может менять знак только в точках, где она равна 0 (нулю), или не существует.
4. Функция элементарная, поэтому непрерывная на ОДЗ: (-∞; 1) U (1; ∞).

Разрыв: х = 1;

limx³ : (1- x)² = ∞ - Разрыв 2-го рода (бесконечный), поэтому есть вертикальная асимптота в точке 1;

х = 1 - уравнение асимптоты вертикальной.

5. y’ = x²(3 - x) : (1 - x)³;

ОДЗ (y’): x ≠ 1;

х = 1 - точка критическая.

y’ = 0;

0; 3 - точки критические.

6. y’’ = 6x : (1 - x)⁴;

Критические т.: 1, 0;

x = 0 - т. перегиба, y(0) = 0.

7. limx³ : (1 - 2x + x²) = ∞ - нет горизонтальной асимптоты, но может быть наклонная.

k = 1 – число;

b = 2 – число.

Следовательно, есть асимптота наклонная y = x + 2 на + ∞ и на - ∞.

Пример 2

Дано y = (x² + 1) : (x - 1). Произвести исследование. Построить график.

1. Область существования - вся числовая прямая, кроме т. x = 1.

2. y пересекает OY (если это возможно) в т. (0;g(0)). Находим y(0) = -1 - т. пересечения OY.

Точки пересечения графика с OX находим, решив уравнение y = 0. Уравнение корней действительных не имеет, поэтому эта функция не пересекает OX.

3. Функция непериодическая. Рассмотрим выражение

g(-x) ≠ g(x), и g(-x) ≠ -g(x). Это означает, что это общего вида функция (ни четная, ни нечетная).

4. Т. x = 1 разрыв имеет второго рода. Во всех остальных точках функция непрерывна.

5. Исследование функции на экстремум:

(x² - 2x - 1) : (x - 1)² = y'

и решим уравнение y' = 0.

Итак, 1 - √2, 1 + √2, 1 - точки критические или точки возможного экстремума. Эти точки разбивают числовую прямую на четыре интервала.

На каждом интервале производная имеет определенный знак, который можно установить методом интервалов или вычисления значений производной в отдельных точках. На интервалах (-∞; 1 - √2) U (1 + √2; ∞), положительная производная, значит, функция растет; если xє(1 - √2; 1) U (1; 1 + √2), то функция убывает, потому что на этих интервалах производная отрицательная. Через т. x₁ при переходе (движение следует слева направо) изменяет производная знак с "+" на "-", поэтому, в этой точке есть локальный максимум, найдем

y_max = 2 - 2√2.

При переходе через x₂ изменяет производная знак с "-" на "+", поэтому, в этой точке есть локальный минимум, причем

y_mix = 2 + 2√2.

Т. x = 1 не т. экстремума.

6. 4 : (x - 1)³ = y''.

На (-∞; 1) 0 > y'', следственно, на этом интервале кривая выпуклая; если xє(1; ∞) - кривая вогнута. В точке 1 не определена функция, поэтому эта точка не точка перегиба.

7. Из результатов пункта 4 следует, что x = 1 - асимптота вертикальная кривой.

Горизонтальные асимптоты отсутствуют.

x + 1 = y - асимптота наклонная данной кривой. Других асимптот нет.

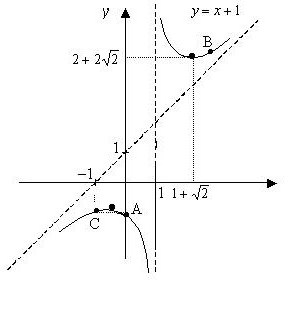
8. Учитывая проведенные исследования, строим график (см. рисунок выше).