Метод конечных элементов и его применение

Метод конечных элементов возник как один из приемов исследования различных конструкций. В настоящее время он повсеместно признан как общий способ решения широкого круга задач в различных областях техники.

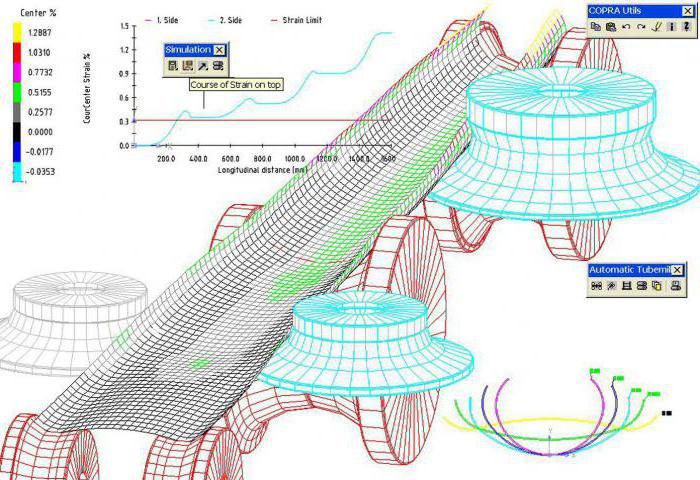
Определение

Инженерный анализ методом конечных элементов заключается в аппроксимации сплошной среды с бесконечно большими числами степеней свободы совокупностью элементов (подобластей), имеющих конечные числа степеней свободы. Между этими элементами устанавливается взаимосвязь. Признание метода объясняется простотой его математической формы и физического толкования.

Применение в механике

Метод конечных элементов в механике разрушения и в задачах строительной механики выражается как соотношение МКЭ в форме перемещений. Вначале задаются в рамках каждого элемента так называемые функции формы. Они определяют перемещение во внутренней области элемента по перемещению в узлах. Последние – это точки, где сочетаются конечные элементы.

Неизвестными МКЭ являются возможные и независимые перемещения узлов конечно элементной модели (КЭМ). Таким образом, КЭМ конструкции представляет собой систему закрепленных узлов. Дополнительные связи соотносятся с направлением возможных перемещений узлов.

Суть метода

По своей сути элементная модель конструкции аналогична основной системе классического метода перемещений, которая применяется при расчете стержневых систем. Для достижения восприимчивой точности результатов расчетов по методу конечных элементов приходится уменьшать размеры элементов, увеличивая тем самым точность аппроксимации геометрических характеристик и функций перемещений в пределах конечного элемента.

КЭМ сложных конструкций достигают сотен и даже миллионов степеней свободы, а потому метод конечных элементов в технике является машинно-ориентированным, реализация которого возможна только посредством компьютеров.

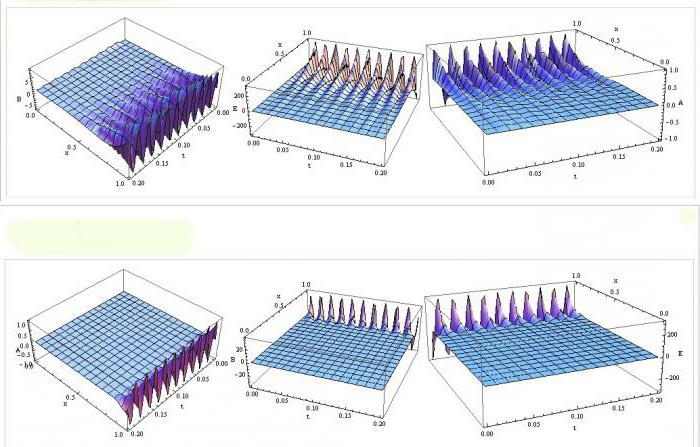
Практическая реализация

Для применения МКЭ на практике необходимо разбираться не только в теории механики, но и обладать знаниями в области программирования. Применение метода конечных элементов зачастую строится на базе вариационных принципов механики, в основе которых заложены два фундаментальных скаляра: потенциальная и кинетическая энергия упругой конструкции. Определение этих скаляров, независимых от выбранной системы координат, позволяет записывать соотношение МКЭ в инвариантной форме.

Для обеспечения удобства программирования соотношения МКЭ записываются в компактной матричной, или тензорной форме. На сегодня моделирование методом конечных элементов достаточно полно математически обосновано, созданы высокоэффективные программные продукты, которые все время совершенствуются вместе со средствами программирования.

Учебно-вычислительные программы

Технический прогресс, особенно в области ЭВМ, существенно изменил взгляды на постановку и решение инженерных задач. Построение расчетной модели тесно связано с процессом вычислений, и разделить эти два этапа на пути получения практических результатов почти невозможно.

Метод конечных элементов широко применяется в инженерной практике, что также способствовало включению его в учебные программы вузов. МКЭ предоставляет способы построения математической модели исследуемого явления исходя из его физической сущности.

Первые учебники по МКЭ были написаны сложным языком, но вскоре методика преподавания была упрощена благодаря внедрению специализированных программ. Например, хорошо себя зарекомендовал программный комплекс «Ассистент». Он позволяет проверить знания студентов в интерактивном режиме и способствует развитию навыков работы с программными продуктами при решении практических задач.

Расчет линейных деформаций

Сегодня основы метода конечных элементов базируются на том, что величины и понятия, ему присущие, не вводятся заранее, а вытекают из существа задачи строительной механики. Круг проблем, которые можно решать с помощью МКЭ, практически неограничен. Рассмотрим для примера задачу по расчету линейной деформации упругих конструкций от действия статических нагрузок.

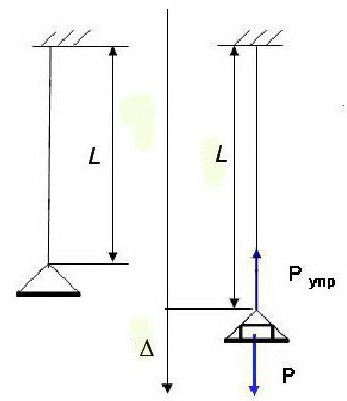
Английский физик Р. Гук провел исследования деформаций центрально-нагруженных стержней, выполненных из разных упругих материалов, под действием статической силы: ∆=Pl/EA.

Он также установил зависимость между величинами, определяющими этот процесс: σ=Eε, где деформация выражена соотношением ε=∆/l, напряжение обозначено как σ=P/A (здесь A – площадь сечения стержня).

Коэффициент пропорциональности E определяет упругие характеристики материала и имеет физическую суть – напряжение, соответствующее единичной деформации.

Влияние статической силы

Статически действующая сила растет во времени постепенно (G≥P≥0). Перемещения, которые она порождает, тоже растут постепенно, без ускорений.

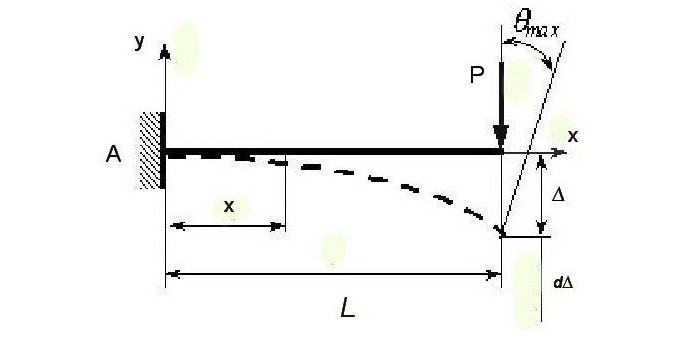
Анализ методом конечных элементов позволяет определить воздействие статической силы на перемещение, учитывая, что эти показатели меняются. Возрастанию (приросту) силы на бесконечно маленькую величину dP соответствует возрастание (прирост) перемещения d∆. Работа силы (P+∆P) на перемещение d∆ имеет значение dA=(P+∆P)×d∆.

Окончательное значение работы силы определяется по формуле A=∫Pd∆.

Введем зависимость между разномерными величинами под знаком интеграла ∆=Pα, где α – коэффициент податливости, который выражает физическую сущность перемещения точки, к которой добавлена единичная сила, в направлении этой силы. Соотношение ∆=Pα устанавливает единицу измерения α (м/Н). Отсюда следует, что d∆=dPα.

Коэффициенту податливости соответствует другая важная характеристика конструкции – коэффициент жесткости k=l/α (н/м), который определяет силу, вызывающую единичное перемещение конструкции в направлении этой силы.

С учетом всех характеристик и коэффициентов итоговое уравнение принимает вид: A=∫PdPα = α×(P²/2)=(G∆)/2.

Получена формула Клапейрона, которая определяет действительную работу статически действующей силы на перемещение, ею же порожденное в упругом теле. По этой методике рассчитываются и другие численные методы.

Метод конечных элементов для стержневых систем

Стержень является пространственным телом, два размера которого, ширина и высота, гораздо меньше длины. Это дает возможность рассматривать его физическую модель в виде линии, проходящей через центры сечений. Если внешние силы, приложенные к стержню, расположены в одной плоскости с его моделью, то можно считать, что деформации его происходят в этой же плоскости.

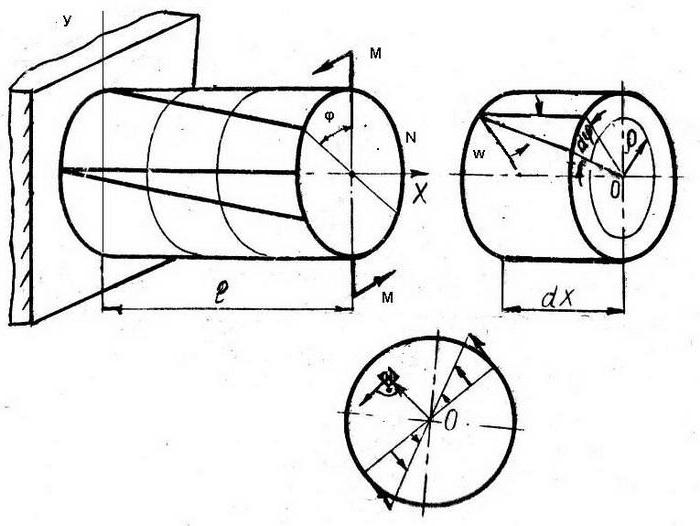
С математической точки зрения геометрические характеристики перемещения и напряжения в пределах стержня являются функциями одного аргумента. Соотношения теории упругости базируются на гипотезе плоских сечений стержня. Связь между деформациями и напряжениями соответствует линейному закону Гука. В каждом сечении стержня проявляются три плоскости перемещения:

• координата u – продольная сила;
• координата w – прогиб;
• координата φ – угол поворота.

При этом продольная u и прогиб w независимы, а угол поворота выражается формулой φ=dw/dx, где dw – величина прогиба после воздействия на стержень внешней силы, dx – участок прогиба (определяемый значением w+dw).

Для бесконечно малой величины стержня dx действует соотношение dx=dφ×P.

Потенциальную энергию деформации стержня естественно вычислять в локальной системе координат, ось x которой совпадает с осью стержня, а ось y перпендикулярна оси стержня: U=½∫N×du+½∫M×dφ=½∫N×(du/dx)dx+½∫M×(d²w/dx²)dx.

Изопараметрический подход в МКЭ

Рассмотрим применение метода конечных элементов в изопараметрической системе конечных элементов плоско-напряженной конструкции. Процесс создания конечно элементной модели конструкций состоит из нескольких этапов, первым из которых является построение сетки конечных элементов (КЭ), выбор глобальной системы координат относительно целой конструкции и локальной системы, связанной с конечным элементом.

Ответственным этапом является определение функций формы, которые обеспечивают определение перемещений в пределах конечного элемента из-за перемещения его узлов. Есть разные способы построения функций формы, но они должны обеспечить выполнение нескольких условий по аппроксимации функций перемещений.

• Выполнение условий неразрывности перемещений не только в узлах конечных элементов, но и на их границах.
• Обеспечение сохранения производных от функций перемещений, которые относятся к упругому потенциалу.
• Движение перемещения конечного элемента как жесткого целого. Это означает, что при смещении элемента как твердого тела компоненты вектора деформаций равны нулю.

Проблемы и решения

Теория методов конечных элементов гласит, что соотношения МКЭ формируются в локальной системе координат. Поэтому перечисленные требования относительно функций формы выполняются автоматически, если оси локальной системы ориентированы по сторонам конечного элемента. Такие случаи имеют место для конечных элементов стержневых конструкций, прямоугольных стеновых панелей, прямоугольных плит.

Но на практике встречаются конструкции с контуром произвольного определения. В этом случае приходится выполнять преобразование для аппроксимации перемещений в глобальной системе координат, что приводит к разрывам перемещений на границах конечных элементов и, как следствие, – к потере точности приближенных расчетов.

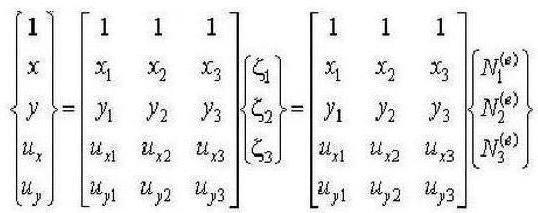
Возникла идея отобразить плоский четырехугольный конечный элемент общего вида на квадрат с локальной системой координат, начало которой находится в центре этой фигуры, и осями, ориентированными по его сторонам. Для дальнейшего использования конечных элементов в форме квадрата необходимо установить взаимно однозначную связь между локальными координатами произвольного четырехугольного КЭ и локальной системой координат КЭ в форме квадрата. Ведь для квадратного конечного элемента функции формы строятся достаточно просто.

Метод конечных элементов для расчета пластин

Пластина – это вставка или цилиндрическое тело, высота которого значительно меньше размеров в плане. Размер по высоте называется толщиной пластины. Плоскость, которая делит высоту пластины пополам, называется срединной или базовой плоскостью. Линия пересечения боковой поверхности со срединной плоскостью называется контуром пластины.

Тонкой считается пластина, для которой отношение толщины к меньшему размеру в плане находится в пределах h≤L/5, где h – толщина пластины, L – ее ширина.

Пластина считается жесткой, если под действием поперечной нагрузки наибольший ее прогиб при деформации не превышает 1/5 толщины.

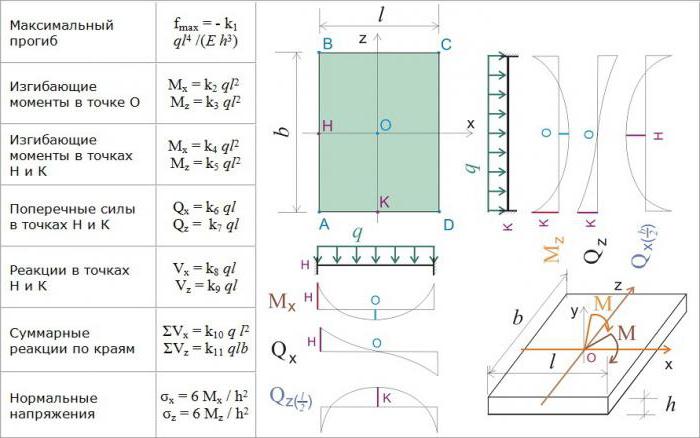
При расчете методом КЭ сначала вводят систему координат: X₁, X₂ и X₃. Начала осей X₁ и X₂ расположены в срединной плоскости. Ось X₃ ориентируют по нормали к срединной плоскости.

Расчеты обычно сводятся к вычислению перемещения (сдвига) пластины в некоей точке под воздействием нагрузок (сил). В произвольной точке пластины, которая рассматривается как трехмерное тело, проявляются три направления перемещения: U₁, U₂, U₃. Определяющим является перемещение по нормали к срединной плоскости, которое называется прогибом и обозначается буквой W.

Расчеты считаются выполненными, если от заданной нагрузки (а это обычно равномерно распределенная, направленная к поверхности) установлен способ вычисления перемещений U и сдвига W в произвольной точке пластины. Соотношения МКЭ строятся на основе положений технической теории упругости, предложенных физиком Кирхгофом.

Гипотезы Кирхгофа

Метод конечных элементов во многом основывается на гипотезах, сформулированных в 1845 немецким физиком Г. Киргофом. Гипотеза прямых нормалей утверждает, что любая прямая линия, нормальная к срединной плоскости недеформированной пластины, остается прямой и нормальной к срединной поверхности деформированной пластины, а длина прямой линии не меняется. Суть ее заключается в отсутствии сдвига между слоями пластины по толщине.

Если оси декартовых координат размещены так, что плоскости X₁, X₂ совпадают со срединной плоскостью, то из первой части гипотезы вытекают следующие равенства: y₁₃=0, y₂₃=0. Гипотеза о неизменности длины прямой линии предполагает, что линейная деформация в направлении оси X₃ равна нулю: ε₃₃=0.

Гипотеза об отсутствии давления между слоями пластины, параллельными срединной поверхности, предполагает, что напряжениями σ₃₃ по сравнению с напряжениями σ₁₁ и σ₂₂ можно пренебречь, то есть σ₃₃=0.

Гипотеза о недеформируемости срединной плоскости предполагает, что в срединной плоскости пластины отсутствуют деформации растяжения, сжатия и сдвига. То есть срединная плоскость является нейтральной. Так что в ней перемещения U₁=U₂=0.

Вывод

Метод конечных элементов, широко применяемый в строительстве и механике, позволяет рассчитывать смещения различных элементов, подвергающихся определенным нагрузкам. Система, сформулированная еще в 1936 году советскими учеными, начала широко применяться лишь спустя десятилетия, так как требовала большого объема расчетов. С внедрением ЭВМ эта задача упростилась.