Формулы объемов призм треугольных различных видов

Любое твердое тело в трехмерном пространстве обладает некоторым объемом. Вычислением этой характеристики геометрических фигур занимается стереометрия. В данной статье рассмотрим, что такое призма треугольная, и по какой формуле объем призмы треугольной может быть рассчитан.

Треугольная призма

Эта фигура относится к классу призм, поэтому она, как любой представитель этого класса, состоит из двух одинаковых и параллельных оснований и параллелограммов. Основаниями являются треугольники произвольного типа (равносторонние, равнобедренные, прямоугольные и другие), боковые же стороны могут быть произвольными параллелограммами, ромбами, квадратами и прямоугольниками. Число боковых сторон равно трем. Рисунок ниже демонстрирует, о какой фигуре пойдет речь.

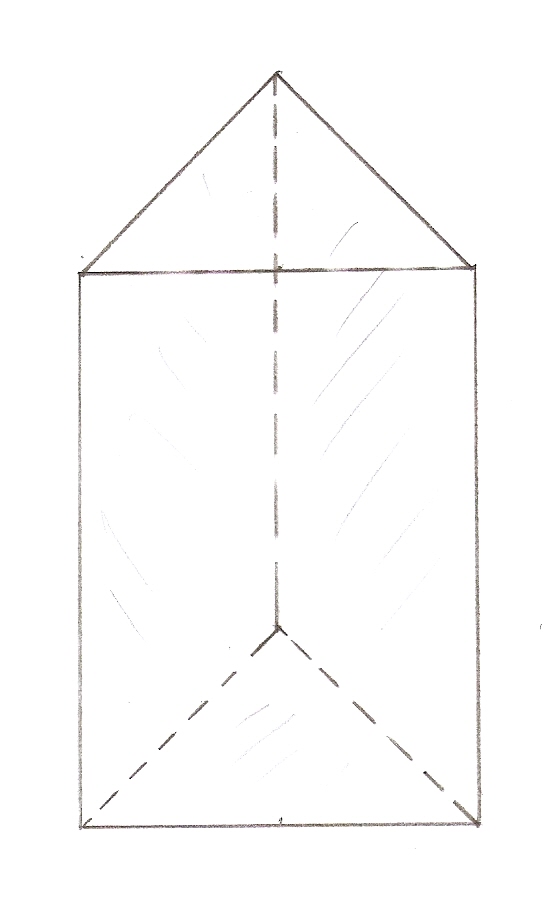
На этом рисунке мы видим геометрическую фигуру, которая состоит из пяти сторон, девяти ребер и шести вершин. Стороны мы уже охарактеризовали. Что касается ребер, то любое из них можно отнести к одному из двух типов: либо ребро принадлежит одному из оснований (в этом случае оно является стороной треугольного основания), либо оно образовано пересечением боковых граней (боковое ребро). Важным свойством призмы является равенство всех ее боковых ребер.

Все треугольные призмы классифицируются по двум признакам:

• прямые и наклонные;
• правильные и неправильные.

Прямая призма обладает прямоугольными боковыми сторонами. Если ее основания будут равносторонними треугольниками, тогда она будет правильной. Далее мы приведем формулы объема призмы треугольной прямой, правильной фигуры, призмы с прямоугольным треугольником и фигуры наклонной.

Как рассчитывать объем фигуры произвольного типа?

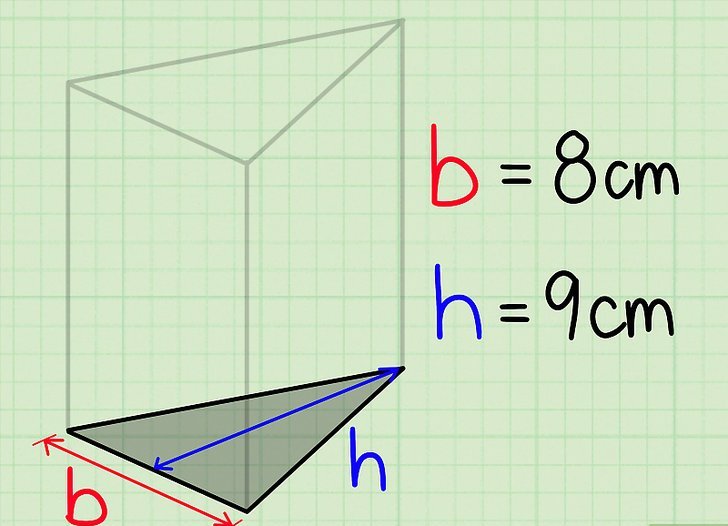
Часть пространства, которая ограничена плоскими сторонами геометрической фигуры, называется ее объемом. В общем случае для призмы абсолютно любого типа справедлива следующая формула для определения ее объема:

V = S_o × h

Как видно, она очень проста и содержит всего два множителя: S_o - площадь одного основания, h - высота призмы, то есть дистанция между ее основаниями.

Применительно к треугольной призме произвольной формы (наклонной и неправильной), для вычисления величины S_o можно воспользоваться универсальной формулой для треугольника:

S_o = 1 / 2 × h_a × a

Здесь a - сторона треугольника, h_a - высота треугольника, опущенная на сторону a.

Расчет высоты h призмы можно провести с использованием теоремы Пифагора, если знать длину бокового ребра b и двугранные углы между основанием и боковыми гранями.

Формула объема треугольной призмы правильной

Многогранник, который мы изучаем, будет правильным, если две его грани являются одинаковыми треугольниками равносторонними и три грани - это одинаковые прямоугольники. Формулу для объема такой призмы несложно получить из выражения общего вида, записанного в пункте выше. Чтобы это сделать, рассчитаем сначала площадь основания:

S_o = 1 / 2 × h_a × a = 1 / 2 × √3 / 2 × a × a = √3 / 4 × a²

Значение высоты треугольника h_a получено, исходя из того факта, что для равностороннего основания она является также медианой и биссектрисой. Таким образом, площадь S_o является функцией только одного параметра (стороны a).

Формулу объема для изучаемой призмы можно получить, если умножить на высоту выражение выше:

V = √3 / 4 × a² × h

Поскольку для рассматриваемой фигуры высота равна длине бокового ребра b, то полученное выражение также можно переписать через параметры a и b.

Объем прямой фигуры с прямоугольным треугольником в основании

Прямоугольный треугольник представляет собой фигуру из трех сторон, две из которых пересекаются под прямым углом. Эти стороны называются катетами. Обозначим их a₁ и a₂. Третья сторона называется гипотенузой (a₃). Из планиметрии известно каждому школьнику, что если взять половину произведения катетов, то можно получить площадь рассматриваемого треугольника, то есть:

S_o = a₁ × a₂ / 2

Так как призма является прямой, то достаточно умножить на S_o длину ее бокового ребра b, чтобы получить объем фигуры:

V = a₁ × a₂ × b/2

Объем правильной фигуры через значение ее диагонали

Треугольная призма является самой простой фигурой из своего класса, поэтому она обладает всего одним единственным типом диагонали. Это диагонали трех ее параллелограммов.

Предположим, что имеется правильная фигура, диагональ которой равна d (это диагональ прямоугольника), а высота равна h. Как рассчитать ее объем?

Для начала следует определить значение стороны основания a. Для этого воспользуемся теоремой Пифагора:

d² = h² + a² =>

a = √(d² - h²)

Тогда формула объема треугольной призмы приобретает вид:

V = √3 / 4 × a² × h = √3 / 4 × (d² - h²) × h

В случае правильной призмы объем всегда является функцией двух параметров (h и d в данном выражении).