Принцип Дирихле: задачи с решениями

В математике существует множество принципов. Некоторые из них достаточно просты и понятны даже новичку, а некоторые требуют определенных объяснений и доказательств. Однако все они весьма эффективны, и их легко можно применять на практике. Одним из них является принцип Дирихле (известный также как принцип голубей/кроликов). Это достаточно простое утверждение, способное помочь в решении многих математических задач.

История

Данный принцип был сформулирован почетным немецким математиком Иоганном Дирихле еще в 1834 году. Сегодня его применяют в комбинаторике, а также в математической физике. В переводе с оригинального немецкого он звучит как «принцип ящиков». Свои исследования ученый проводил с кроликами и контейнерами. Он продемонстрировал, что если поместить, допустим, 5 кроликов в 7 контейнеров, то, по крайней мере, в одном контейнере будет находиться 5/7 от одного животного. Однако кролика нельзя разделить на части, следовательно, хотя бы одна клетка будет пустовать (5/7 равно 0 целых). Точно так же и в обратную сторону, если кроликов 7, а ящиков 5, то хотя бы в одном из них - 2 кролика (7/5 равно 2 целых). Отталкиваясь от этого утверждения, математику удалось сформулировать принцип, который обеспечивает успешное решение задач по математике уже многие годы.

Современная формулировка и доказательство

На сегодняшний день существует несколько разных формулировок данного принципа. Самая понятная и простая подразумевает, что нельзя посадить 8 кроликов в 3 клетки так, чтобы в каждой было не больше 2. Более научная и сложная формулировка, объясняющая принцип Дирихле, гласит: если в k ячеек находится k+1 зайцев, то, по крайней мере, в 1 ячейке будет располагаться больше одного зайца. А если в k ячеек находится k-1 зайцев, то по крайней мере в 1 ячейке будет располагаться меньше одного зайца. Доказательство этого утверждения совсем простое, так сказать, от противного. Если предположить, что в каждой ячейке располагается зайцев меньше, чем k-1/k, тогда в k ячеек зайцев меньше чем k*k-1/k = k-1, а это противоречит первоначальным условиям.

В действительности такой простой и понятный принцип значительно облегчает решение задач по математике и доказательства многих трудоемких теорем. Просто необходимо учитывать, что зайцев и ячейки можно легко заменить на математические предметы и объекты (цифры, точки, отрезки, фигуры и т. д.).

Еще одна формулировка

Иногда задачи на принцип Дирихле - не такие простые и очевидные, как с животными в ящиках. Необходимо переносить этот принцип на математические множества, чтобы отыскать какие-либо решения. В таком случае можно опираться на другую, более сложную формулировку.

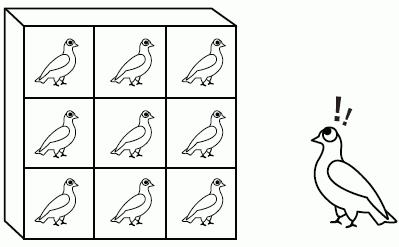
Если отобразить множество S, содержащее d+1 элементов, в множество R с совокупностью d элементов, то два элемента из множества S будут иметь одинаковый образ.

Хотя современные ФГОС по математике предъявляют к ученикам творческие требования и предлагают нестандартные варианты, решение через утверждение Дирихле не всегда такое простое и понятное. Иногда очень трудно определить, какую величину считать животным, а какую – клеткой, и каким образом факт наличия двух животных в одной клетке поможет решению задачи. Да и если удастся в этом разобраться, все равно нельзя определить, в какой именно клетке будет находиться объект. То есть можно просто доказать существование такой ячейки, но нельзя конкретизировать ее.

Пример № 1. Геометрия

Современные примеры решения задач демонстрируют, что животными и клетками могут выступать совершенное различные математические предметы.

Задача

Прямая k проходит через плоскость треугольника ABC, однако не пересекает ни одну его вершину. Необходимо доказать, что она не может пересекать три его стороны.

Решение

Представим, как прямая k разбивает треугольник на две плоскости, назовем их s1 и s2. Будем считать, что s1 и s2 открытые, то есть не содержащие прямую k. Ну а сейчас - самое время применить принцип Дирихле. Задачи с решениями могут продемонстрировать, что под кроликами и ячейками в современных условиях подразумеваются разнообразные объекты. Так, вместо зайцев мы подставим вершины треугольника, а вместо ячеек – полуплоскости. Поскольку проведенная прямая k не пересекает ни одну из вершин, то каждая из них находится в той или иной плоскости. Но поскольку вершины в треугольнике три, а плоскости у нас всего две (s1 и s2), то одна из них будет содержать две вершины. Предположим, что это вершины A и B, и находятся они в полуплоскости s2 (то есть лежат по одну сторону от k). В таком случае отрезок АВ не пересекает прямую k. То есть в треугольнике есть сторона, которую прямая k не пересекает.

Альтернативное решение

В данной задаче мы предположили, что в одной плоскости находятся точки А и В, однако принцип Дирихле не указывает конкретную ячейку, поэтому точно так же мы могли указать, что в одной плоскости разместились вершины С и В, или А и С. Для данной задачи совсем не важно, какую сторону треугольника не пересекает прямая k. Поэтому указанный принцип идеально подходит для ее решения.

Пример № 2. Геометрия

Задача

В середине равностороннего треугольника АВС (у которого АВ = ВС = АС = 1) разместилось 5 точек. Необходимо доказать, что две из них располагаются на расстоянии меньше 0,5.

Решение

Если провести в правильном треугольнике АВС средние линии, они разделят его на 4 маленьких правильных треугольника со сторонами ½ = 0,5. Предположим, что эти треугольники – ячейки, а точки внутри них – кролики. Получается, у нас есть 5 кроликов и 4 ячейки, следовательно, в одной из них будет находиться как минимум два кролика. Учитывая то, что точки не являются вершинами (так как они располагаются внутри треугольника АВС, а не на одной из его сторон), они будут размещаться внутри маленьких фигур. Следовательно, расстояние между ними будет меньше, чем 0,5 (поскольку величина отрезка внутри треугольника никогда не превышает величины его самой большой стороны).

Пример № 3. Комбинаторика

В других областях также можно удачно применять принцип Дирихле: комбинаторика и математическая физика уже давно опираются на него при решении задач.

Задача

Допустим, вокруг округлённого стола стоят на равном расстоянии друг от друга m флажков разных стран, а за столом сидят m представителей от каждой страны, причем каждый из них расположился рядом с чужим флажком. Нужно доказать, что при определенном вращении стола хотя бы двое из представителей окажутся возле своих флажков.

Решение

Получается, что существует m-1 способов развернуть стол так, чтобы изменилось взаиморасположение представителей и флажков (если исключить начальное размещение стола), но при этом остается m представителей.

Применим к решению утверждение Дирихле и обозначим, что представители выступают кроликами, а определенные положения стола при вращении – ячейками. При этом нужно провести аналогию между расположением представителя рядом с соответствующем флажком и заполненными ячейками. То есть положительный результат (1 представитель размешается возле своего флажка) равносилен результату «кролик оказывается в клетке». Мы понимаем, что у нас на одну ячейку меньше, чем нужно (m-1), а значит, в одной из них окажется как минимум 2 кролика. При этом не исключены ситуации, что какая-то клетка будет пустой (ни один представитель не совпал с флажком), а в какой-то клетке окажется два, три или даже больше кроликов (два, три и больше представителей совпадут с флажками). Таким образом, при одном определенном вращении как минимум два представителя очутятся возле своих флажков (как минимум два кролика попадут в одну ячейку).

Приступая к решению такой задачи, важно понимать, что начальное положение – это тоже ячейка, но по условию задачи она заведомо пустует, поэтому мы уменьшаем общее количество на 1 (m-1).

Пример № 4. Теория чисел

Принцип Дирихле в теории чисел также имеет огромное значение.

Задача

Предположим, на листике тетради в клетку ученик произвольно в узлах клеточек проставил 5 точек. Необходимо доказать, что как минимум один отрезок с вершинами в этих точках пройдет через узел клеточки.

Решение

Для начала нужно изобразить на листе тетради систему координат, основа которой расположится в одном из узлов. Оси системы координат будут совпадать с линиями сетки, а за единичный отрезок принята сторона клеточки. Получается, что все 5 отмеченных точек будут находиться в системе, а их координаты будут только целым числом (четным или нечетным). Таким образом, мы получим 4 варианта координат: (четный; четный), (нечетный; четный), (четный; нечетный) и (нечетный; нечетный). А значит, 2 из 5 точек будут соответствовать одному варианту. Если посмотреть на ситуацию с позиции Дирихле, то необходимо обозначить точки как зайцев, а варианты координат - как ячейки. Мы получаем 5 зайцев и 4 клетки, соответственно, в одной из них будет минимум 2 животных. Допустим, это точки Р и А, с координатами (x₄, y₃) и (x₅, y₆). Середина отрезка, соединяющего эти две вершины, будет иметь координаты ((x₄+x₅) / 2), ((y₃+y₆) / 2)), которые будут целыми числами в условиях соответствующей четности x₄ и x_5, y₃ и y₆. Получается, что середина отрезка расположилась в узле клетки.

Пример № 5

Достаточно много задач разной сложности можно решить через принцип Дирихле. Задачи с решениями разнообразных математических и логических вопросов достаточно часто опираются на этот принцип.

Задача

На прямой дороге вырыты маленькие поперечные канавки. Расстояние между всеми канавками одинаковое и равно оно Ö2 м. Необходимо доказать, что, независимо от ширины канавок, человек, шагающий по дороге с интервалом 1 м, однажды попадет ногой в одну из них.

Решение

Для того чтобы облегчить решение, необходимо вообразить, что дорогу можно «намотать» на окружность длиной в Ö2 метров. Получается, что все канавки сольются в 2 противоположных, а шаги человека будут отображаться в форме дуги, равной 1 м. Нам необходимо последовательно отметить все шаги, пока один из них не окажется в дуге, обозначающей канавку, независимо от того, какая будет длина k дуги (ширина канавки). Конечно, очевидно, что если бы человек шагал на расстояние, равное меньше, чем k, то он рано или поздно наступил бы в канаву. Ведь у человека никак не получится переступить расстояние k, если длина его шага меньше, чем k. А значит, нам необходимо найти два следа, расстояние между которыми не будет превышать величину k. Для этого уместно будет воспользоваться принципом Дирихле. Мы мысленно разделим всю окружность на дуги размером меньше k и будем считать их ячейками. Допустим, их окажется n штук. Предположим, что число шагов будет больше чем число дуг (n + m), хотя никакие два шага не будут совпадать из-за иррациональности числа Ö2, тогда по принципу Дирихле, по крайней мере, в одной из ячеек разместится больше одного шага. А поскольку длина дуги составляет меньше k, то и расстояние между шагами будет меньше. Таким образом, мы обнаружили необходимые для доказательства шаги.

Обобщение принципа

Материалы по математике, кроме стандартных (простых и не очень) формулировок, содержат также одну обобщенную, которая используется для выявления более двух объектов, похожих друг на друга. Она утверждает, что если dm + 1 кроликов поместить в d ячеек, то как минимум m + 1 кролик окажется в одной ячейке.

Пример № 6. Обобщение

Задача

Прямоугольник с площадью 5 х 6 клеток (30 клеток), закрашенных только 19. Можно ли обнаружить квадрат площадью 2 х 2 клетки, в котором минимум три будут закрашены?

Решение

Нашу фигуру необходимо разделить на 6 блоков по 5 клеток. Исходя из утверждения Дирихле, в одной из них будет закрашено не менее 4 клеточек (19/6 = 4). Тогда в одном из квадратов площадью 4 клеточки, расположенном в одном из блоков, будет закрашено минимум 3 клетки.

Пример № 7

Класс, в котором 25 человек. Из любых случайно выбранных 3 учеников двое будут друзьями. Необходимо доказать, что в классе находится школьник, у которого больше 11 приятелей.

Два решения вопроса

Для начала возьмем двух школьников, которые не дружат с друг другом (поскольку если бы все они дружили между собой, то в каждой тройке было бы три друга и каждый ученик дружил бы с 24 другими). Оставшиеся 23 одноклассника будут дружить с одним из нашей двойки, поскольку в противном случае нашлась бы тройка, где нет друзей (а это противоречит изначальному условию задачи). Получается, что один из двух школьников будет дружить как минимум с 12 учениками. В данном случае ученики – это кролики, а условия "друзья они или нет" – это ячейки. Мы имеем 23 животных и только 2 клетки. Соответственно, в одной из них как минимум 23/2 = 11,5, т. е. 12 кроликов. То есть один из 2 выбранных нами учеников будет дружить как минимум с 12 своими одноклассниками (или даже больше). Конечно же, существуют и другие методы решения задачи, однако данный - один из самых понятных и удобных.