Как осуществить деление производных?

При работе с функциями часто приходится учитывать их специфику, производя сложение, умножение или деление производных. Последнее из действий чаще всего вызывает вопросы у обучающегося, поэтому этот аспект стоит рассмотреть подробнее.

Производная частного

Когда выполняется деление производных, формула для преобразования выглядит как разность производной числителя, помноженного на знаменатель, и производной знаменателя, умноженного на числитель, и поделённое на квадрат знаменателя. При этом необходимо учитывать, что значение в нижней части дроби должно быть не равным нулю. При решении первых примеров преобразование производной частного нередко возникает проблема, поэтому лучше всего иметь перед глазами эту формулу:

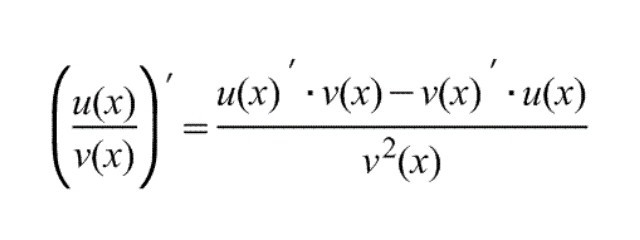
Благодаря этой формуле удаётся привести пример в более простую форму, которую можно разделить на табличные функции производных, после чего решить данную задачу не составит большого труда.

Пример решения

В качестве примера, демонстрирующего ход решения, где выполняется деление производных, стоит рассмотреть следующий:

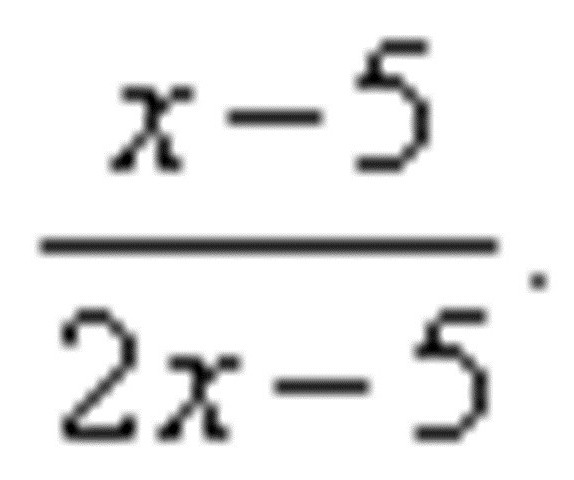
Согласно заданию, необходимо найти производную данного выражения. Воспользовавшись формулой, упрощающей деление производных, преобразуем исходный пример к следующему виду:

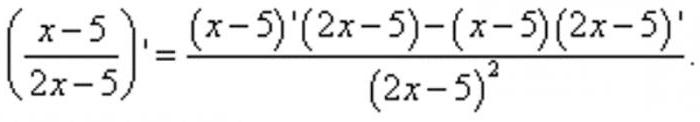
В результате в числителе оказалось две производные табличного вида, значения которых можно вычислить без дополнительных преобразований. В первом случае результатом будет единица, во втором - двойка. Подставив вычисленные данные в пример, получим дробь, в которой останется лишь произвести несложные вычисления в числителе, получив итоговый результат:

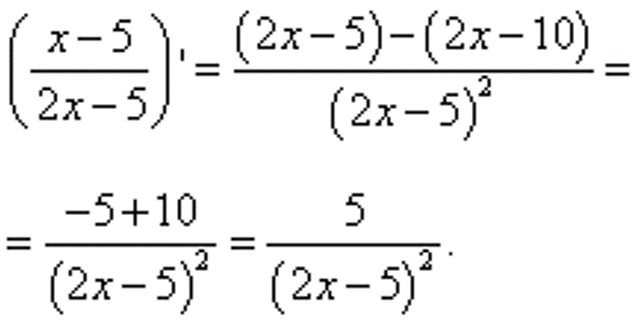
Маленькие хитрости

Перед применением формулы стоит внимательно посмотреть на деление производных. В некоторых случаях дробь можно упростить, благодаря чему приведенная в начале формула может оказаться ненужной или станет более простой. Упрощение дроби можно выполнить несколькими способами, включая деление числителя на знаменатель с целью определения целой части, а также домножением обеих частей дроби на одно и то же ненулевое число - этот приём часто применяется при наличии иррациональности под знаком производной.

Стоит отметить, что перед вначале необходимо проверить пример на наличие решения. Для этого нужно найти область допустимых значений (ОДЗ), и если она будет существовать, не создавая неопределённостей различного вида, можно приступать к вычислениям.