Как вычислить углы между векторами?

При изучении геометрии немало вопросов возникает по теме векторов. Особенные трудности обучающийся испытывает при необходимости найти углы между векторами.

Основные термины

Перед тем как рассматривать углы между векторами, необходимо ознакомиться с определением вектора и понятием угла между векторами.

Вектором называют отрезок, имеющий направление, то есть отрезок, для которого определено его начало и конец.

Углом между двумя векторами на плоскости, имеющих общее начало, называют меньший из углов, на величину которого требуется переместить один из векторов вокруг общей точки, до положения, когда их направления совпадут.

Формула для решения

Поняв, что собой представляет вектор и как определяется его угол, можно вычислить угол между векторами. Формула решения для этого достаточно проста, и результатом её применения будет значение косинуса угла. Согласно определению, он равен частному скалярного произведения векторов и произведения их длин.

Скалярное произведение векторов считается как сумма помноженных друг на друга соответствующих координат векторов-сомножителей. Длина вектора, или его модуль, вычисляется как квадратный корень из суммы квадратов его координат.

Получив значение косинуса угла, вычислить величину самого угла можно с помощью калькулятора или воспользовавшись тригонометрической таблицей.

Пример

После того как вы разберетесь с тем, как вычислить угол между векторами, решение соответствующей задачи станет простым и понятным. В качестве примера стоит рассмотреть несложную задачу о нахождении величины угла.

Первым делом удобнее будет вычислить необходимые для решения значения длин векторов и их скалярного произведения. Воспользовавшись описанием, представленным выше, получим:

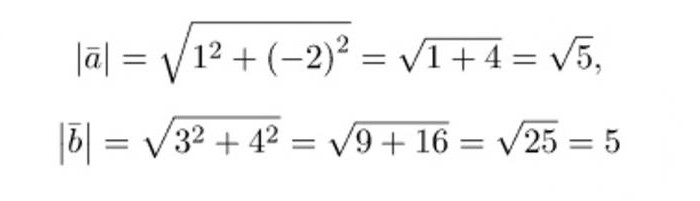
Подставив полученные значения в формулу, вычислим значение косинуса искомого угла:

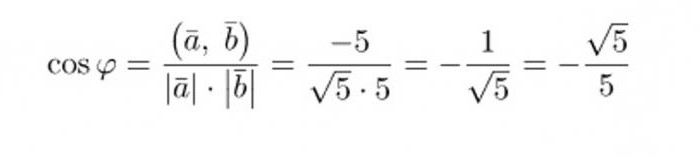
Это число не является одним из пяти распространённых значений косинуса, поэтому для получения величины угла, придётся воспользоваться калькулятором или тригонометрической таблицей Брадиса. Но перед тем, как получить угол между векторами, формула может быть упрощена, чтобы избавиться от лишнего отрицательного знака:

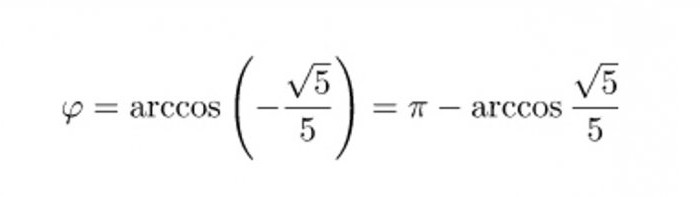
Итоговый ответ для сохранения точности можно оставить в таком виде, а можно вычислить значение угла в градусах. По таблице Брадиса его величина составит примерно 116 градусов и 70 минут, а калькулятор покажет значение 116,57 градуса.

Вычисление угла в n-мерном пространстве

При рассмотрении двух векторов в трёхмерном пространстве, понять, о каком угле идёт речь гораздо сложнее, если они не лежат в одной плоскости. Для упрощения восприятия можно начертить два пересекающихся отрезка, которые образуют наименьший угол между ними, он и будет искомым. Несмотря на наличие третьей координаты в векторе, процесс того, как вычисляются углы между векторами, не изменится. Вычислите скалярное произведение и модули векторов, арккосинус их частного и будет являться ответом на данную задачу.

В геометрии нередко встречаются задачи и с пространствами, имеющими больше трёх измерений. Но и для них алгоритм нахождения ответа выглядит аналогично.

Разница между 0 и 180 градусами

Одна из распространённых ошибок при написании ответа на задачу, рассчитанную на то чтобы вычислить угол между векторами, - решение записать, что векторы параллельны, то есть искомый угол получился равен 0 или 180 градусам. Этот ответ является неверным.

Получив по итогам решения значение угла 0 градусов, правильным ответом будет обозначение векторов как сонаправленных, то есть у векторов будет совпадать направление. В случае получения 180 градусов векторы будут носить характер противоположно направленных.

Специфические векторы

Найдя углы между векторами, можно встретить один из особых типов, помимо описанных выше сонаправленных и противоположно направленных.

• Несколько векторов параллельных одной плоскости называются компланарными.
• Векторы, одинаковые по длине и направлению, называются равными.
• Векторы, лежащие на одной прямой, независимо от направления, именуются коллинеарными.
• Если длина вектора равна нулю, то есть его начало и конец совпадают, то его называют нулевым, а если единице, то единичным.