Тригонометрия с нуля: основные понятия, история

Синус, косинус, тангенс – при произнесении этих слов в присутствии учеников старших классов можно быть уверенным, что две трети из них потеряют интерес к дальнейшему разговору. Причина кроется в том, что основы тригонометрии в школе преподаются в полном отрыве от реальности, а потому учащиеся не видят смысла в изучении формул и теорем.

В действительности данная область знаний при ближайшем рассмотрении оказывается весьма интересной, а также прикладной – тригонометрия находит применение в астрономии, строительстве, физике, музыке и многих других областях.

Ознакомимся с основными понятиями и назовем несколько причин изучить этот раздел математической науки.

История

Неизвестно, в какой момент времени человечество начало создавать будущую тригонометрию с нуля. Однако документально зафиксировано, что уже во втором тысячелетии до нашей эры египтяне были знакомы с азами этой науки: археологами найден папирус с задачей, в которой требуется найти угол наклона пирамиды по двум известным сторонам.

Более серьезных успехов достигли ученые Древнего Вавилона. На протяжении веков занимаясь астрономией, они освоили ряд теорем, ввели особые способы измерения углов, которыми, кстати, мы пользуемся сегодня: градусы, минуты и секунды были заимствованы европейской наукой в греко-римской культуре, в которую данные единицы попали от вавилонян.

Предполагается, что знаменитая теорема Пифагора, относящаяся к основам тригонометрии, была известна вавилонянам почти четыре тысячи лет назад.

Название

Дословно термин «тригонометрия» можно перевести как «измерение треугольников». Основным объектом изучения в рамках данного раздела науки на протяжении многих веков был прямоугольный треугольник, а точнее – взаимосвязь между величинами углов и длинами его сторон (сегодня с этого раздела начинается изучение тригонометрии с нуля). В жизни нередки ситуации, когда практически измерить все требуемые параметры объекта (или расстояние до объекта) невозможно, и тогда возникает необходимость недостающие данные получить посредством расчётов.

Например, в прошлом человек не мог измерить расстояние до космических объектов, а вот попытки эти расстояния рассчитать встречаются задолго до наступления нашей эры. Важнейшую роль играла тригонометрия и в навигации: обладая некоторыми знаниями, капитан всегда мог сориентироваться ночью по звездам и скорректировать курс.

Основные понятия

Для освоения тригонометрии с нуля требуется понять и запомнить несколько основных терминов.

Синус некоторого угла – это отношение противолежащего катета к гипотенузе. Уточним, что противолежащий катет – это сторона, лежащая напротив рассматриваемого нами угла. Таким образом, если угол составляет 30 градусов, синус этого угла всегда, при любом размере треугольника, будет равен ½. Косинус угла – это отношение прилежащего катета к гипотенузе.

Тангенс – это отношение противолежащего катета к прилежащему (либо, что то же самое, отношение синуса к косинусу). Котангенс – это единица, деленная на тангенс.

Стоит упомянуть и знаменитое число Пи (3,14…), которое представляет собой половину длины окружности с радиусом в одну единицу.

Популярные ошибки

Люди, изучающие тригонометрию с нуля, совершают ряд ошибок – в основном по невнимательности.

Во-первых, при решении задач по геометрии необходимо помнить, что использование синусов и косинусов возможно только в прямоугольном треугольнике. Случается, что учащийся «на автомате» принимает за гипотенузу самую длинную сторону треугольника и получает неверные результаты вычислений.

Во-вторых, поначалу легко перепутать значения синуса и косинуса для выбранного угла: напомним, что синус 30 градусов численно равен косинусу 60, и наоборот. При подстановке неверного числа все дальнейшие расчёты окажутся неверными.

В-третьих, пока задача полностью не решена, не стоит округлять какие бы то ни было значения, извлекать корни, записывать обыкновенную дробь в виде десятичной. Часто ученики стремятся получить в задаче по тригонометрии «красивое» число и сразу же извлекают корень из трёх, хотя ровно через одно действие этот корень можно будет сократить.

Этимология слова «синус»

История слова «синус» поистине необычна. Дело в том, что буквальный перевод этого слова с латыни означает «впадина». Всё потому, что верное понимание слова затерялось при переводе с одного языка на другой.

Названия базовых тригонометрических функций произошли из Индии, где понятие синуса обозначалось словом «тетива» на санскрите - дело в том, что отрезок вместе с дугой окружности, на которую он опирался, походил на лук. Во времена расцвета арабской цивилизации индийские достижения в области тригонометрии были заимствованы, и термин перешел в арабский язык в виде транскрипции. Случилось так, что в этом языке уже было похожее слово, обозначающее впадину, и если арабы понимали фонетическую разницу между родным и заимствованным словом, то европейцы, переводящие научные трактаты на латынь, по ошибке буквально перевели арабское слово, никакого отношения к понятию синуса не имеющее. Им мы и пользуемся по сей день.

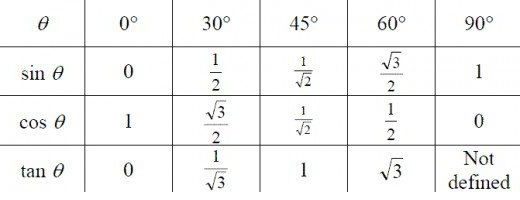
Таблицы значений

Существуют таблицы, в которые занесены числовые значения для синусов, косинусов и тангенсов всех возможных углов. Ниже представим данные для углов в 0, 30, 45, 60 и 90 градусов, которые необходимо выучить как обязательный раздел тригонометрии для «чайников», благо запомнить их довольно легко.

Если случилось так, что числовое значение синуса или косинуса угла «вылетело из головы», есть способ вывести его самостоятельно.

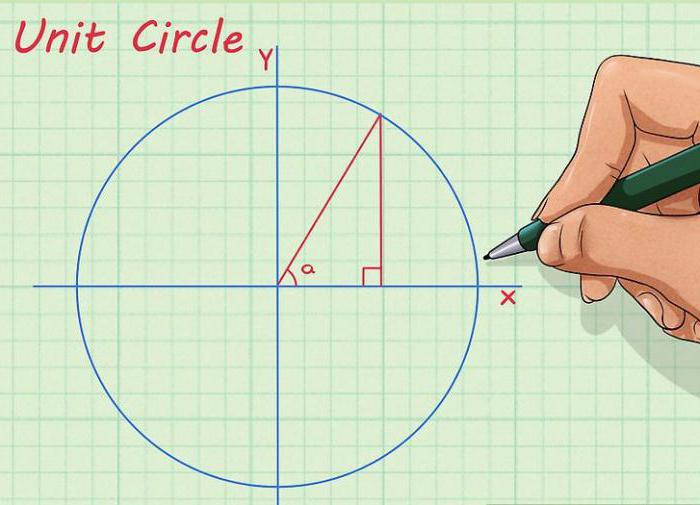
Геометрическое представление

Начертим круг, через его центр проведем оси абсцисс и ординат. Ось абсцисс располагается горизонтально, ось ординат – вертикально. Обычно они подписываются как «X» и «Y» соответственно. Теперь из центра окружности проведем прямую таким образом, чтобы между ней и осью X получился нужный нам угол. Наконец, из той точки, где прямая пересекает окружность, опустим перпендикуляр на ось X. Длина получившегося отрезка будет равна численному значению синуса нашего угла.

Данный способ весьма актуален, если вы забыли нужное значение, например, на экзамене, и учебника по тригонометрии под рукой нет. Точной цифры вы таким образом не получите, но разницу между ½ и 1,73/2 (синус и косинус угла в 30 градусов) вы точно увидите.

Применение

Одними из первых специалистов, использующих тригонометрию, были моряки, не имеющие никакого другого ориентира в открытом море, кроме неба над головой. Сегодня капитаны кораблей (самолётов и других видов транспорта) не ищут кратчайший путь по звёздам, зато активно прибегают к помощи GPS-навигации, которая без использования тригонометрии была бы невозможна.

Практически в каждом разделе физики вас ждут расчёты с использованием синусов и косинусов: будь то приложение силы в механике, расчёты пути объектов в кинематике, колебания, распространение волн, преломление света – без базовой тригонометрии в формулах просто не обойтись.

Ещё одна профессия, которая немыслима без тригонометрии – это геодезист. Используя теодолит и нивелир либо более сложный прибор – тахиометр, эти люди измеряют разницу в высоте между различными точками на земной поверхности.

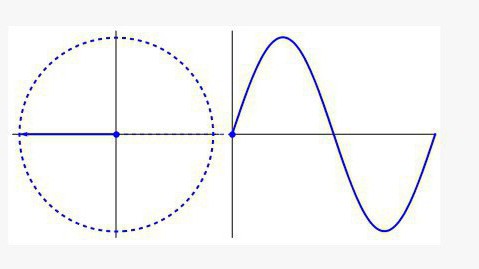
Повторяемость

Тригонометрия имеет дело не только с углами и сторонами треугольника, хотя именно с этого она начинала своё существование. Во всех областях, где присутствует цикличность (биологии, медицине, физике, музыке и т. д.) вы встретитесь с графиком, название которого наверняка вам знакомо - это синусоида.

Такой график представляет собой развёрнутую вдоль оси времени окружность и внешне похож на волну. Если вы когда-нибудь работали с осциллографом на занятиях по физике, вы понимаете, о чем идет речь. Как музыкальный эквалайзер, так и прибор, отображающий сердечные ритмы, используют формулы тригонометрии в своей работе.

В заключение

Задумываясь о том, как выучить тригонометрию, большинство учащихся средней и старшей школы начинают считать её сложной и непрактичной наукой, поскольку знакомятся лишь со скучной информацией из учебника.

Что касается непрактичности - мы уже увидели, что в той или иной степени умение обращаться с синусами и тангенсами требуется практически в любой сфере деятельности. А что касается сложности… Подумайте: если люди пользовались этими знаниями больше двух тысяч лет назад, когда взрослый человек имел меньше знаний, чем сегодняшний старшеклассник, реально ли изучить данную область науки на базовом уровне лично вам? Несколько часов вдумчивых занятий с решением задач – и вы достигнете своей цели, изучив базовый курс, так называемую тригонометрию для «чайников».