Разложение квадратных трехчленов на множители: примеры и формулы

Разложение квадратных трехчленов на множители относится к школьным заданиям, с которыми рано или поздно сталкивается каждый. Как его выполнить? Какова формула разложения квадратного трехчлена на множители? Разберемся пошагово с помощью примеров.

Общая формула

Разложение квадратных трехчленов на множители осуществляется решением квадратного уравнения. Это несложная задача, которую можно решить несколькими методами - нахождением дискриминанта, при помощи теоремы Виета, существует и графический способ решения. Первые два способа изучаются в средней школе.

Общая формула выглядит так: lx²+kx+n=l(x-x₁)(x-x₂) (1)

Алгоритм выполнения задания

Для того чтобы выполнить разложение квадратных трехчленов на множители, нужно знать теорему Вита, иметь под рукой программу для решения, уметь находить решение графически или искать корни уравнения второй степени через формулу дискриминанта. Если дан квадратный трехчлен и его надо разложить на множители, алгоритм действий такой:

1) Приравнять исходное выражение к нулю, чтобы получить уравнение.

2) Привести подобные слагаемые (если есть такая необходимость).

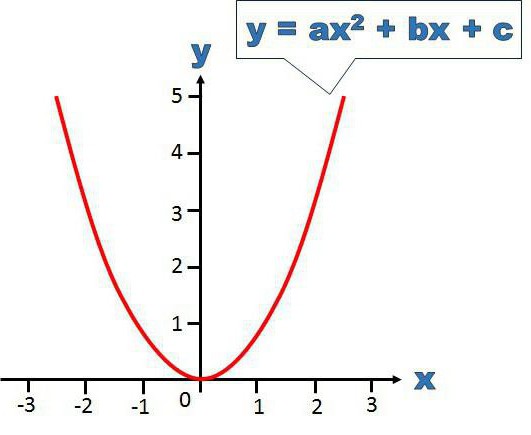
3) Найти корни любым известным способом. Графический метод лучше применять в случае, если заранее известно, что корни - целые и небольшие числа. Нужно помнить, что количество корней равно максимальной степени уравнения, то есть у квадратного уравнения корней два.

4) Подставить значение х в выражение (1).

5) Записать разложение квадратных трехчленов на множители.

Примеры

Окончательно понять, как выполняется это задание, позволяет практика. Иллюстрируют разложение на множители квадратного трехчлена примеры:

необходимо разложить выражение:

х²-17х=-32

Прибегнем к нашему алгоритму:

1) х²-17х+32=0

2) подобные слагаемые сведены

3) по формуле Виета найти корни для этого примера сложно, потому лучше воспользоваться выражением для дискриминанта:

D=289-128=161=(12,69)²

x₁=2,155

x₂=14,845

4) Подставим найденные нами корни в основную формулу для разложения:

(х-2,155)_*(х-14,845)

5) Тогда ответ будет таким:

х²-17х+32=(х-2,155)(х-14,845)

Проверим, соответствуют ли найденные дискриминантом решения формулам Виета:

2,155+14,845=17

14,845^.2,155=32

Для данных корней применяется теорема Виета, они были найдены правильно, а значит полученное нами разложение на множители тоже правильно.

Аналогично разложим 12х²+7х-6.

12х²+7х-6=0

D=337

x₁=-7+(337)^1/2

x₂=-7-(337)^1/2

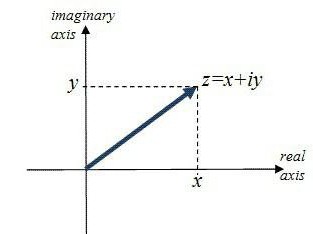
В предыдущем случае решения были нецелыми, но действительными числами, найти которые легко, имея перед собой калькулятор. Теперь рассмотрим более сложный пример, в котором корни будут комплексными: разложить на множители х²+4х+9. По формуле Виета корни найти не получится, и дискриминант отрицательный. Корни будут на комплексной плоскости.

D=-20

Исходя из этого, получаем нтересующие нас корни -4+2i*5^1/2 и -4-2i_*5^1/2 , поскольку (-20)^1/2=2i*5^1/2.

Получаем искомое разложение, подставив корни в общую формулу.

Еще один пример: нужно разложить на множители выражение 23х²-14х+7.

Имеем уравнение 23х²-14х+7=0

D=-448

Значит, корни 14+21,166i и 14-21,166i. Ответ будет такой:

23х²-14х+7=23(х-14-21,166i )*(х-14+21,166i ).

Приведем пример, решить который можно без помощи дискриминанта.

Пусть нужно разложить квадратное уравнение х²-32х+255. Очевидно, его можно решить и дискриминантом, однако быстрее в данном случае подобрать корни.

x₁=15

x₂=17

Значит х²-32х+255=(х-15)(х-17).