Условие равновесия рычага. Правило моментов. Простые механизмы. Задачи и решения

С незапамятных времен человечество использует разные механизмы, которые призваны облегчить физический труд. Одним из них является рычаг. Что он собой представляет, в чем заключается идея его использования, а также каково условие равновесия рычага, рассмотрению всех этих вопросов посвящена данная статья.

Когда человечество стало применять принцип рычага?

Точно ответить на этот вопрос трудно, поскольку простые механизмы уже были известны древним египтянам и жителям Месопотамии еще в трехтысячном году до нашей эры.

Одним из таких механизмов является так называемый рычаг-журавль. Представлял он собой длинный шест, который располагался на опоре. Последняя устанавливалась ближе к одному концу шеста. К концу, который дальше находился от опорной точки, привязывали сосуд, на другой клали некоторый противовес, например, камень. Система настраивалась таким образом, чтобы наполненный наполовину сосуд приводил к горизонтальному положению шеста.

Рычаг-журавль служил для подъема воды из колодца, реки или другого углубления до уровня, где находился человек. Прикладывая небольшую силу к сосуду, человек опускал его к источнику воды, сосуд наполнялся жидкостью, а затем, прилагая небольшое усилие к другому концу шеста с противовесом, можно было поднять указанный сосуд.

Легенда об Архимеде и корабле

Всем известен древнегреческий философ из города Сиракузы, Архимед, который в своих трудах не только описал принцип действия простых механизмов (рычаг, наклонная доска), но и привел соответствующие математические формулы. До настоящего времени остается знаменитой его фраза:

Дайте мне точку опоры, и я сдвину этот мир!

Как известно, такой опоры никто ему не предоставил, и Земля осталась на своем месте. Однако, что действительно смог сдвинуть Архимед, так это корабль. Одна из легенд Плутарха (работа "Параллельные жизни") говорит следующее: Архимед в письме своему другу, царю Гиерону Сиракузскому, говорил, что смог бы в одиночку переместить сколь угодно большой вес, при определенных условиях. Гиерон был удивлен таким заявлением философа и попросил, чтобы он продемонстрировал то, о чем говорит. Архимед согласился. В один из дней корабль Гиерона, находящийся в доке, был загружен людьми и наполненными водой бочками. Философ, расположившись на некотором расстоянии от корабля, смог его поднять над водой, потянув за веревки, прикладывая при этом небольшое усилие.

Составные части рычага

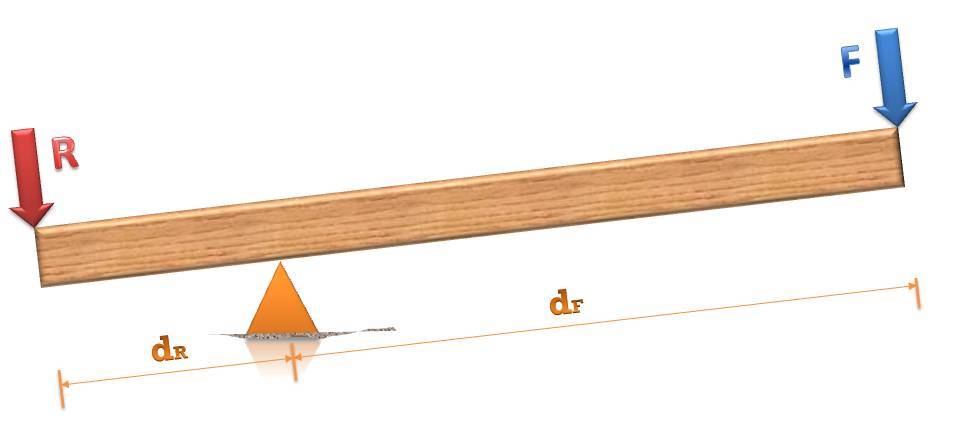
Несмотря на то, что речь идет о достаточно простом механизме, он все же имеет определенное устройство. Физически он состоит из двух основных частей: шест или балка и опора. При рассмотрении же задач шест рассматривают как объект, состоящий из двух (или одного) плеча. Плечо - это часть шеста, которая находится относительно опоры с одной стороны. Большую роль в принципе работы рассматриваемого механизма играет именно длина плеча.

Когда рассматривают рычаг в работе, то возникает еще два дополнительных элемента: прилагаемая сила и сила противодействия ей. Первая стремится привести в движение объект, создающий силу противодействия.

Условие равновесия рычага в физике

Познакомившись с устройством этого механизма, приведем математическую формулу, используя которую, можно сказать, какое из плеч рычага и в каком направлении будет двигаться или, наоборот, все устройство будет находиться в состоянии покоя. Формула имеет вид:

F₁ * l₁ = F₂ * l₂,

где F₁ и F₂ - силы действия и противодействия, соответственно, l₁ и l₂ - длины плеч, к которым приложены эти силы.

Это выражение позволяет исследовать условия равновесия рычага, имеющего ось вращения. Так, если плечо l₁ больше, чем l₂, тогда для уравновешивания силы F₂ понадобится меньшее значение F₁. Наоборот, если l₂ > l₁, то для противодействия силе F₂ потребуется приложить большую F₁. Эти выводы можно получить, если переписать выражение выше в следующей форме:

F₁ / F₂ = l₂ / l₁.

Как видно, участвующие в процессе формирования равновесия силы находятся в обратной зависимости от длины плеч рычага.

В чем состоит выигрыш и проигрыш при использовании рычага?

Из приведенных выше формул следует важный вывод: с помощью длинного плеча и малого усилия можно перемещать объекты с огромной массой. Это действительно так, и многие могут подумать, что применение рычага приводит к выигрышу в работе. Но это не так. Работа - это энергетическая величина, которая не может быть создана из ничего.

Проанализируем работу простого рычага, имеющего два леча l₁ и l₂. Пусть на конце плеча l₂ помещен груз весом P (F₂ = P). На конец другого плеча человек прилагает силу F₁ и поднимает этот груз на высоту h. Теперь, вычислим работу каждой силы и приравняем полученные результаты. Получим:

F₁ * x = F₂ * h.

Сила F₂ действовала вдоль вертикальной траектории длиной h, в свою очередь F₁ действовала также вдоль вертикали, но уже была приложена к другому плечу, конец которого переместился на неизвестную величину x. Чтобы ее найти, необходимо подставить в последнее выражение формулу связи между силами и плечами рычага. Выражая x, имеем:

x = F₂ * h / F₁ = l₁ * h / l₂.

Это равенство показывает, если l₁ > l₂, тогда F₂ > F₁ и x > h, то есть, прикладывая небольшую силу, можно поднять груз с большим весом, но при этом придется переместить соответствующее плечо рычага (l₁) на большее расстояние. Наоборот, если l₁ < l₂, то F₂ < F₁ и x < h, то есть груз некоторого веса можно поднять на большую высоту h, перемещая плечо l₁ на меньшую амплитуду, но при этом придется приложить достаточно большую силу F₁. В первом случае получается выигрыш в силе, во втором в пути или скорости.

Таким образом, рычаг не дает выигрыш в работе, он позволяет лишь перераспределить ее либо в пользу меньшей прилагаемой силы, либо в пользу большей амплитуды перемещения объекта. В обсуждаемой теме физики работает общий философский принцип: всякий выигрыш компенсируется некоторым проигрышем.

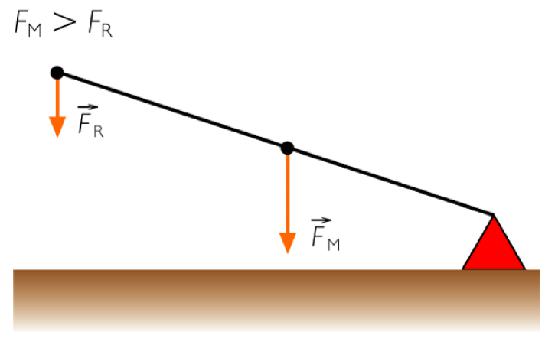
Виды рычагов

В зависимости от точек приложения силы и от положения опоры различают следующие виды этого механизма:

• Первого рода: точка опоры находится между двумя силами F₁ и F₂, поэтому от длины плеч будет зависеть то, в чем дает выигрыш такой рычаг. Примером являются обычные ножницы.
• Второго рода. Здесь сила, против которой совершается работа, расположена между опорой и прилагаемым усилием. Такой тип конструкции означает, что он всегда будет давать выигрыш в силе и проигрыш в пути и скорости. Его примером является садовая тачка.
• Третьего рода. Последний вариант, который остается реализовать в этой простой конструкции, это положение прилагаемого усилия между опорой и силой противодействия. В этом случае получается выигрыш в пути, но проигрыш в силе. Примером может служить пинцет.

Понятие о моменте силы

Рассмотрение любых проблем в механике, которые включают понятия оси или точки вращения, осуществляется с помощью правила моментов сил. Поскольку опора рычага - это тоже ось (точка), вокруг которой поворачивается система, то для оценки равновесия этого механизма также используется момент силы. Под ним понимается величина в физике, равная произведению плеча на действующую силу, то есть:

M = l * F.

Учитывая это определение, условие равновесия рычага можно переписать в следующем виде:

M₁ = M₂, где M₁ = l₁ * F₁ и M₂ = l₂ * F₂.

Момент M обладает аддитивностью, это означает, что общий момент силы для рассматриваемой системы можно получить путем обычного сложения всех действующих на нее моментов M_i. Однако при этом следует учитывать их знак (сила, вызывающая вращение системы против часовой стрелки, создает положительный момент +M, и наоборот). С учетом сказанного, правило моментов для рычага, находящегося в равновесии, будет выглядеть так:

M₁ - M₂ = 0.

Рычаг теряет свое равновесие, когда M₁ ≠ M₂.

Где используется принцип рычага?

Выше уже были приведены некоторые примеры использования этого простого и известного с древних времен механизма. Здесь лишь перечислим несколько дополнительных примеров:

• Плоскогубцы: рычаг 1-го рода, который позволяет создавать огромные усилия за счет небольшой длины плеч l₂, где находятся зубья инструмента.
• Открывалка крышек банок и бутылок: это рычаг 2-го рода, поэтому он всегда дает выигрыш в прилагаемом усилии.
• Удочка: рычаг 3-го рода, который позволяет перемещать конец удочки с поплавком, грузилом и крючком на большие амплитуды. Проигрыш при этом в силе ощущается, когда рыбаку оказывается трудно вытащить рыбу из воды, даже если ее масса не превышает 0,5 кг.

Сам человек с его суставами, мышцами, костями и сухожилиями - это яркий пример системы с множеством разных рычагов.

Решение задачи

Условие равновесия рычага, рассмотренное в статье, используем для решения простой задачи. Необходимо вычислить приблизительную длину плеча рычага, прилагая усилие к концу которого, Архимед смог поднять корабль, как это описывает Плутарх.

Для решения введем следующие предположения: во внимание примем греческую трирему в 90 тонн водоизмещением и положим, что опора рычага находилась в 1 метре от ее центра массы. Поскольку Архимед, согласно легенде, легко смог поднять корабль, то будем считать, что для этого он приложил силу, равную половине своего веса, то есть около 400 Н (для массы 82 кг). Тогда, применяя условие равновесия рычага, получаем:

F₁ * l₁ = F₂ * l₂ => l₁ = F₂ * l₂ / F₁ = m * g * l₂ / F₁ = 90000 * 9,81 * 1/400 ≈ 2,2 км.

Даже если увеличить прилагаемую силу до значения веса самого Архимеда и приблизить опору еще в два раза, то получится значение длины плеча около 500 метров, что также является большой величиной. Скорее всего, легенда Плутарха - это преувеличение с целью продемонстрировать эффективность рычага, и Архимед в действительности не поднимал корабль над водой.