Алгебраическая прогрессия: формулы и примеры решений

В данной статье будет рассмотрена алгебраическая прогрессия, формулы, необходимые для решения задач с ее участием, а также некоторые примеры их использования. Для полноты информации кратко будет сказано о другом виде прогрессии - геометрической.

Понятие об алгебраической прогрессии

Всякий ряд чисел, который упорядочен согласно некоторому закону, может называться прогрессией. Наиболее популярными и применяемыми для решения практических задач являются два вида таких рядов: алгебраическая и геометрическая прогрессия. Рассмотрим подробнее первую из них.

Алгебраическую чаще называют арифметической прогрессией. Математически она означает следующее:

a_n = a_n-1 + d

То есть речь идет о такой числовой последовательности, в которой любой ее член отличается от предыдущего или последующего на одинаковое число d. Это число носит название разности (его можно определить, найдя разность двух соседних элементов прогрессии).

Согласно такому определению, рассматриваемая прогрессия имеет начало, но не имеет конца. Начинается она всегда с члена a₁ (любое действительное число), а затем продолжается путем суммирования этого члена с разностью d. Соответственно, она может быть бесконечно возрастающей (d > 0) или убывающей (d < 0). Ситуация, когда d = 0, также может рассматриваться как частный случай арифметической прогрессии, представленной бесконечной последовательностью одинаковых чисел.

Формула для нахождения произвольного члена

Как было пояснено выше, рассматриваемый вид прогрессии однозначно определяется ее первым элементом и разностью, однако это правило распространяется на любые другие величины. Например, знание двух произвольных элементов или одного элемента и суммы некоторого числа членов также однозначно определяет прогрессию.

Для вычисления n-го элемента можно с успехом пользоваться следующей формулой:

a_n = a₁ + (n - 1) * d

Очевидность справедливости этого выражения не вызывает сомнения, и его может проверить каждый, подставляя малые значения n.

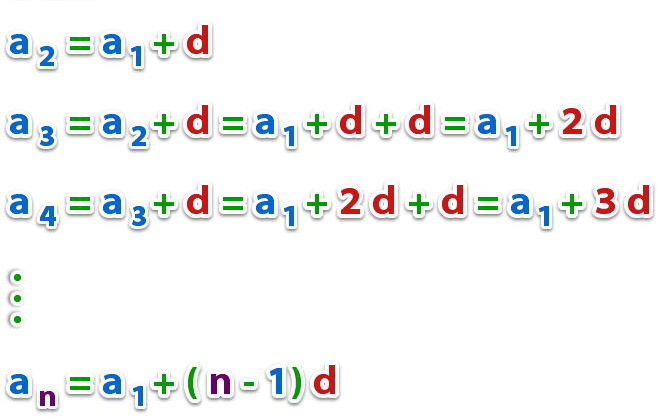
Формула для восстановления прогрессии по двум известным элементам

В школьном курсе алгебры такие задачи являются типичными на прогрессию: известно два элемента a_n и a_m, причем n > m, необходимо на них построить всю прогрессию.

Решается эта проблема с использованием формулы для n-го члена. Выпишем два соответствующих выражения:

a_n = a₁ + (n - 1) * d;

a_m = a₁ + (m - 1) * d

Найдем разность между первым и вторым (знак равенства при этом сохраняется):

a_n - a_m = (n - m) * d =>

d = (a_n - a_m) / (n - m)

Мы видим, как легко можно найти разность прогрессии, если известны два ее члена: для этого необходимо из большего по порядку вычесть меньшее, а затем полученную разность поделить на разность их порядковых номеров.

Как только найдена разность, вычислить первый член не представит никакого труда (для этого следует воспользоваться любым из двух первых выражений).

Сумма прогрессии алгебраической

Еще одной серией типичных задач на прогрессию является нахождение суммы их членов. Ниже приводится соответствующая формула суммы прогрессии алгебраической:

S_n = ∑_i=1ⁿ (a_i) = n * (a₁ + a_n) / 2

То есть для определения суммы первых слагаемых n следует вычислить сумму всего двух из них (первого и n-ного), умножить ее на количество членов n и поделить результат пополам.

Математическое доказательство этого выражения мы опустим, однако логическое доказательство все же приведем. Можно заметить, что ввиду свойства рассматриваемого типа прогрессии всегда выполняется следующее равенство:

a₁ + a_n = a₂ + a_n-1

Действительно, второй член больше первого на d, но на столько же предпоследний (a_n-1) меньше последнего (a_n). В случае парного числа элементов мы получаем ровно половину таких сумм от всего числа элементов (n / 2), откуда и следует приведенная формула для S_n.

Принято считать, что отмеченную особенность арифметической прогрессии впервые установил Карл Гаусс, известный математик конца XVIII - первой половины XIX века, когда он в уме за несколько секунд посчитал сумму натуральных чисел от единицы до 100.

Примеры решения задач

Рассмотрим два примера алгебраической прогрессии.

1. Известно, что 9-й член равен 7, а 21-й равен 51. Необходимо найти первые 5 членов этой арифметической прогрессии.

Условие задачи позволяет сразу же рассчитать разность d, применяя формулу с a_n и a_m, которая записана выше. Имеем:

d = (a_n - a_m) / (n - m) = (51 - 7) / (21 - 9) = 3,667

При получении разности d мы выполнили округление до 3 знака после запятой.

Теперь можно рассчитать первый элемент ряда. Для этого воспользуемся данными для 9 члена:

a₉ = a₁ + d * 8 => a₁ = a₉ - d * 8 = 7 - 3,667 * 8 = -22,336

Для решения задачи осталось сделать последний шаг: последовательно добавить 4 раза величину d к первому элементу. Получаем:

a₁ = -22,336;

a₂ = -22,336 + 3,667 = -18,669;

a₃ = -18,669 + 3,667 = -15,002;

a₄ = -15,002 + 3,667 = -11,335;

a₅ = -11,335 + 3,667 = -7,668

Напомним, что все рассчитанные значения справедливы до третьего знака после запятой.

2. Рабочие складывали спиленные стволы деревьев в виде пирамиды. Известно, что они сложили всего 33 бревна, причем до завершения пирамиды им не хватило всего 3 бревна. Следует определить, сколько рядов бревен сложили рабочие.

Ответ на этот вопрос заключается в решении алгебраической прогрессии, но для того, чтобы к нему приступать, необходимо внимательно разобраться с данным условием.

Во-первых, поскольку бревна складываются в пирамиду, значит, в каждом предыдущем ряду было на одно бревно больше, то есть d = 1. Во-вторых, если известно, что не хватило до завершения пирамиды всего 3 бревна, тогда два верхних ряда остались пустыми:

a₁ = 1, a₂ = a₁ + d = 2, a₁ + a₂ = 3

Учтем эти три бревна, добавив их к 33 уже сложенным, и определим неизвестное число рядов n, пользуясь формулами для суммы и n-го члена:

S_n = n * (a₁ + a_n) / 2; a_n = a₁ + d * (n - 1) =>

S_n = n * (a₁ + a₁ + d * (n - 1)) /2 = (2 * a₁ - d) / 2 * n + d * n² / 2

Подставляем в последнее равенство известные данные и решаем полученное квадратное уравнение относительно n:

36 = 0,5 * n + 0,5 * n² или

n² + n - 72 = 0

Дискриминант: D = 1 - 4 * 1 * (-72) = 289

Корни: n = (-1 ± 17) / 2 = (8; -9)

Отрицательное значение отбросим сразу, поскольку оно противоречит условию задачи. Таким образом, 8 рядов пирамиды будут содержать 36 бревен. Так как рабочие не завершили два верхних ряда, значит, всего они сложили 6 рядов бревен.

Несколько слов о прогрессии геометрической

Алгебраическая и геометрическая прогрессии, как правило, рассматриваются в рамках одной темы, поэтому полезно дать понятие и о втором типе упорядоченного числового ряда. Итак, прогрессия геометрическая представляет собой ряд чисел, которые подчиняются закону:

a_n = a_n-1 * r

То есть в отличие от арифметической, здесь для получения всех элементов необходимо не прибавлять одно число, а умножать на него (r называется знаменателем).

Из определения понятно, что геометрическая прогрессия растет (уменьшается) гораздо быстрее, чем арифметическая.

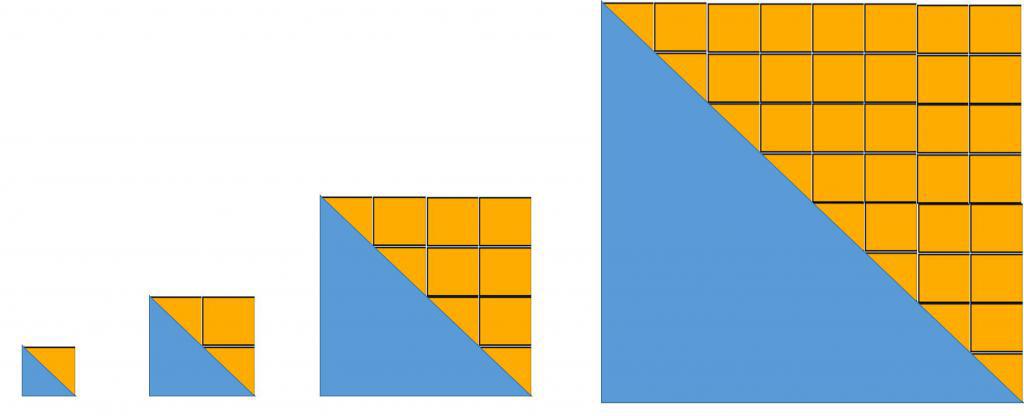
Применяется она часто в геометрии, например при вычислении площадей фигур с помощью их разбиения на отдельные элементы (метод деления пополам).