Свойства и формулы прямоугольной призмы

Призма является одной из совершенных объемных фигур, наряду с шаром, цилиндром и пирамидой, свойства которой рассматриваются в специальном разделе геометрии – стереометрии. В данной статье обсудим основные характеристики прямоугольной призмы.

Фигура призма

Многие знают про треугольные призмы или шестиугольные, но не каждый человек четко представляет, что это за фигура в общем виде. В геометрии под ней понимают пространственный объект, который ограничен двумя одинаковыми многоугольниками и несколькими четырехугольниками. Два многоугольника называются основаниями призмы. Они лежат в параллельных плоскостях. Все четырехугольники являются параллелограммами и образуют боковую поверхность фигуры.

Основные формулы и свойства призмы касаются вопросов определения объема, площади ее поверхности и числа образующих фигуру элементов. В состав последних входят вершины, ребра и грани. Количества этих элементов связаны друг с другом выражением Эйлера для полиэдров. Оно имеет следующий вид:

Число ребер = число граней + число вершин - 2

Поскольку боковая поверхность призмы представлена всегда параллелограммами, то основные ее характеристики зависят от типа многоугольника, лежащего в основаниях этой фигуры. Если многоугольником является треугольник, то призма называется треугольной, если четырехугольник – то четырехугольной и так далее.

Прямоугольная призма

Если угол между каждой боковой стороной призмы и ее основанием равен 90^o, то такая фигура называется прямоугольной. Заметим, что речь идет об угле между сторонами, а не между ребрами. Часто такую фигуру называют прямой призмой.

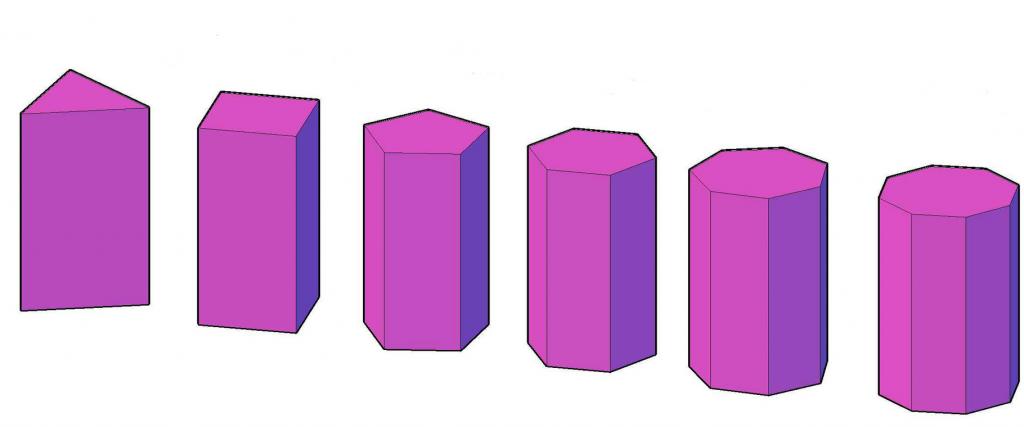
Когда отмеченный угол равен 90^o, то все параллелограммы автоматически становятся прямоугольниками. Это еще одна причина, почему эту призму называют прямоугольной. На рисунке ниже показано, как выглядит прямоугольная призма.

Здесь мы видим, что каждая из трех призм отличается от остальных типом многоугольника, лежащего в основании фигуры. На рисунке приведены треугольная, четырехугольная и пятиугольная призмы. Количество прямоугольников для каждой из них равно 3, 4 и 5 соответственно.

Важным свойством прямоугольной призмы, которое отличает ее от косоугольной, является тот факт, что длина ее бокового ребра совпадает с высотой фигуры. Это свойство оказывается очень удобным при вычислении площади ее поверхности и объема.

Правильная призма

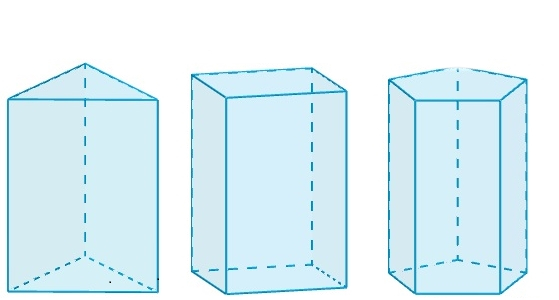
Всякая прямая призма, в основании которой лежит правильный многоугольник, называется правильной. Указанный многоугольник должен иметь одинаковые длины всех сторон и равные углы. Таким прямоугольником является равносторонний треугольник, квадрат, пентагон и так далее.

На рисунке ниже изображены две призмы. Левая из них является правильной, поскольку в ее основании находится квадрат и она прямая. Правая же, несмотря на то, что прямая, правильной не является, поскольку ее основание – это произвольный четырехугольник.

Единственной правильной призмой, которая имеет собственное название, является куб. Он получается, когда высота фигуры совпадает с длиной стороны квадрата, находящегося в основании.

Поскольку площадь для правильного многоугольника вычислить легко, то для любой правильной призмы известны формулы площади ее поверхности и объема.

Площадь правильного многоугольника

Перед тем как приводить формулы площади поверхности и объема призмы прямоугольной, рассмотрим правильный многоугольник.

Ниже на рисунке изображен набор правильных многоугольников, за исключением круга.

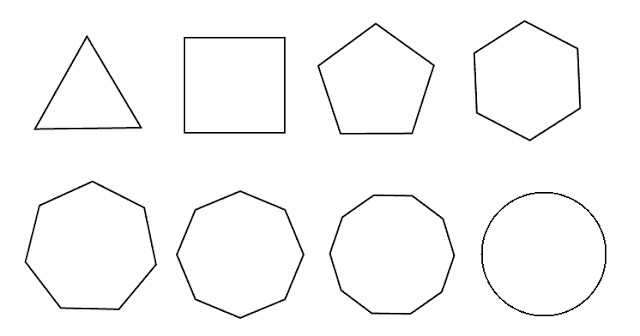
Видно, что для каждого из них число сторон совпадает с количеством углов. Более того, все стороны и углы являются одинаковыми. Эти свойства позволяют привести формулу, которая является универсальной для всех правильных многоугольников и позволяет вычислить их площадь. Формула имеет вид:

S_n = n/4*a²*ctg(pi/n)

Где a – длина стороны, n – количество сторон (вершин) фигуры. Символом ctg обозначается тригонометрическая функция котангенс.

Покажем, как пользоваться этим выражением. Например, вычислим площадь равностороннего треугольника. Для него n = 3, тогда:

S₃ = 3/4*a²*ctg(pi/3) = 3/4*a²*1/√3 = √3/4*a²

Теперь воспользуемся этой формулой для квадрата. Имеем:

S₄ = 4/4*a²*ctg(pi/4) = a²*1 = a²

То есть мы получили всем известное выражение для площади квадрата.

Поверхность призмы

Когда давалось геометрическое определение рассматриваемой фигуры, было показано, что она состоит из двух оснований и некоторого числа параллелограммов. Это число в точности равно количеству сторон многоугольника в основании. Площадь поверхности рассматриваемой фигуры принято записывать следующей формулой:

S = 2*S_o + S_b

Где S_o – основания площадь, S_b – боковой поверхности. Поскольку последняя состоит из n параллелограммов, то ее величина равна сумме их площадей.

В случае правильной прямой призмы боковая поверхность будет образована прямоугольниками со сторонами a и h, где a – длина стороны основания, h – высота призмы. Для случая n правильного угольника, получаем формулу для площади S_tot призмы:

S_tot = n/2*a²*ctg(pi/n) + n*a*h

Ниже приведен рисунок, демонстрирующий развертку шестиугольной призмы.

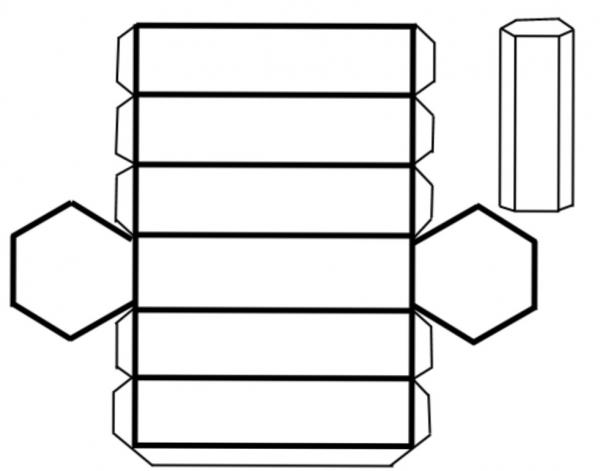
Видно, что фигура образована двумя правильными шестиугольниками и шестью одинаковыми прямоугольниками, одна сторона которых равна стороне шестиугольника. Применяя выражение выше для этой призмы, получим:

S⁶_tot = 6/2*a²*ctg(pi/6) + 6*a*h = 3*a*(√3*a+2*h)

Формула объема

Объем призмы в общем случае вычисляется по следующей простой формуле:

V = S_o*h

Для прямоугольной фигуры высота является ее ребром, поэтому это выражение применять оказывается просто. Например, рассчитаем объем для треугольной правильной призмы. Выше уже была рассчитана площадь ее основания, она равна:

S₃ = √3/4*a²

Тогда значение объема для фигуры будет следующим:

V = S₃*h = √3/4*a²*h

Приведенные формулы для прямой призмы с правильным многоугольником в основании показывают, что все свойства для таких фигур можно получить, если знать всего два параметра: длину стороны n-угольника и высоту призмы.