Высшая математика: плоскость в пространстве

Автор Валерий Савельев November 14, 2018

Вторым после прямой важным элементом пространственной геометрии является плоскость. Умение описывать ее уравнением дает возможность вычисления пространственных углов и высот для различных объемных фигур. В данной статье приведем все виды уравнений, описывающих плоскость в пространстве. Также рассмотрим возможные варианты взаимного расположения плоскостей.

Геометрическое понятие о плоскости

В двумерной геометрии плоскость не рассматривается, поскольку все задачи решаются только в координатах x и y. Когда же мы добавляем третью координатную ось z, то плоскость становится важным геометрическим элементом.

Под понятием "плоскость" понимают совокупность точек, любые две из которых если соединить, то полученный вектор будет всегда перпендикулярен некоторому заданному вектору. Этот заданный вектор называется нормалью. Нормаль играет важную роль при численном описании плоскости, а ее свойства используются для решения различных задач.

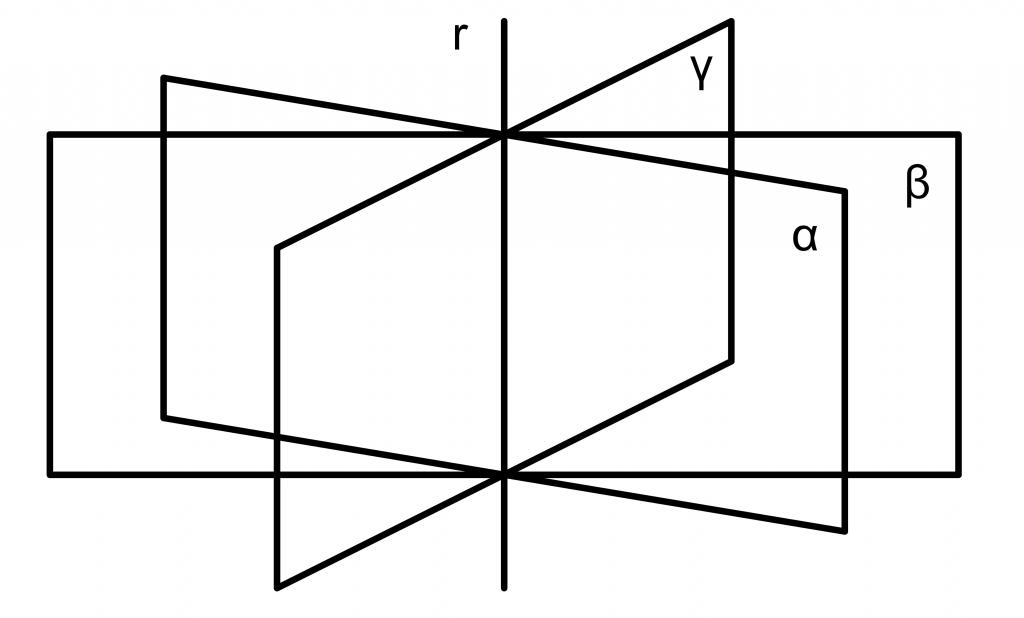
Рисунок ниже показывает три плоскости в пространстве (синие), которые пересекает четвертая (красная).

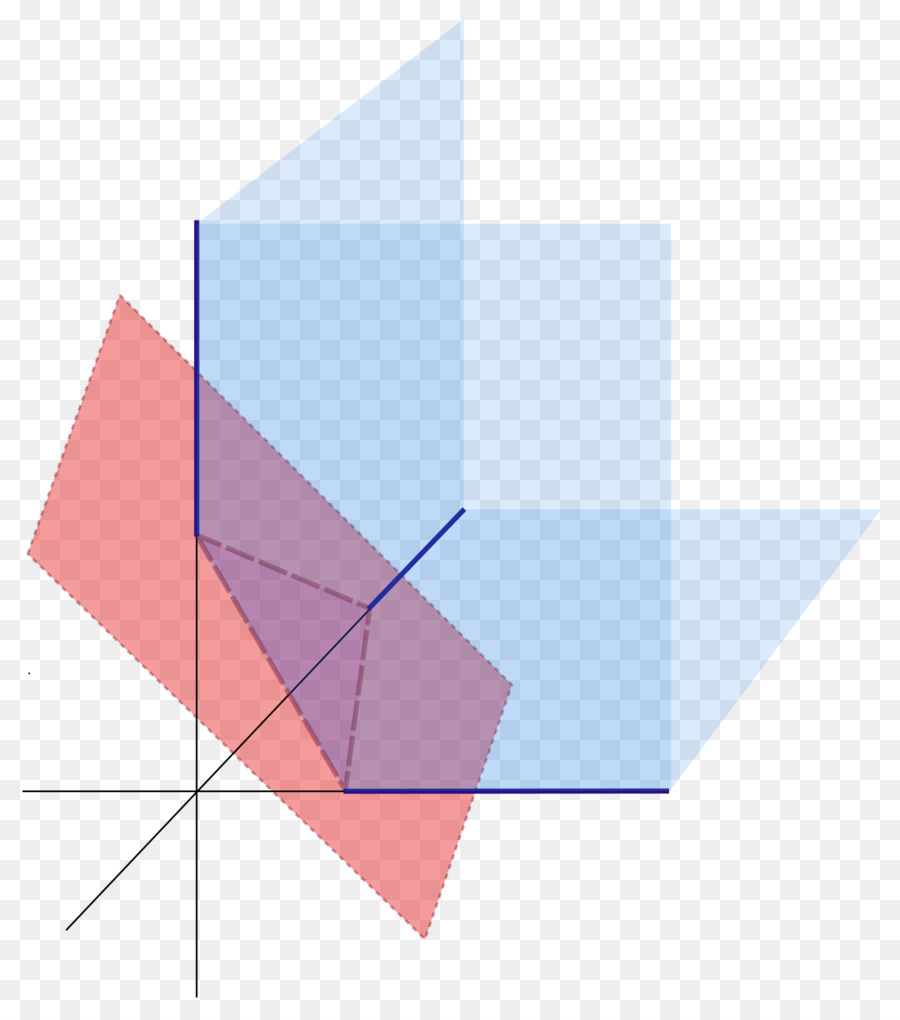
Общее уравнение

Данное выше определение поможет получить уравнение для плоскости в пространстве в координатах. Предположим, что имеется некоторая точка с известными координатами Q(x₀; y₀; z₀). Известно, что она лежит в некоторой плоскости, нормаль к которой равна n¯(A; B; C). Предположим теперь, что произвольная точка M(x; y; z) также принадлежит этой плоскости. Последнее означает, что вектора QM¯ и n¯ будут перпендикулярны, то есть их скалярное произведение зануляется. Поэтому можно записать следующее равенство:

(QM¯*n¯) = 0.

Подставляем в него координаты и раскрываем скобки, приходим к уравнению:

(x-x₀)*A + (y-y₀)*B +(z-z₀)*C = 0 =>
A*x + B*y + C*z + D = 0, где D = -1*(A*x₀ + B*y₀ + C*z₀).

Полученное уравнение для плоскости называется общим. Оно имеет такую же форму, что и общее для прямой уравнение на плоскости. Видно, что коэффициенты, стоящие перед переменными x, y и z представляют собой не что иное, как координаты перпендикулярного плоскости вектора. Он называется направляющим.

Отметим, что если при получении общего уравнения конкретная точка Q неизвестна, а имеется только направляющий вектор n¯, тогда мы приходим к уравнению для совокупности параллельных плоскостей, отличающихся только параметром D.

Уравнение в отрезках

При изображении плоскостей в пространстве, когда заданы конкретные оси координат, проще всего вести геометрические построения, если известны точки, где плоскость пересекает эти оси. Выражение, которое позволяет узнать значения координат пересечения плоскости с осями x, y и z, называется уравнением в отрезках. Его можно получить, проведя некоторые математические преобразования с уравнением общего типа.

Предположим, что известно следующее уравнение:

A*x + B*y + C*z + D = 0.

Перенесем свободный член D в правую часть равенства, а затем поделим обе части уравнения так, чтобы справа получилась единица. Имеем:

A*x + B*y + C*z = -D =>
x/(-D/A) + y/(-D/B) + z/(-D/C) = 1 или
x/p + y/q + z/r = 1, где p = -D/A, q = -D/B, r = -D/C.

Полученное выражение называется в отрезках уравнением, причем отсекаемые на осях x, y и z длины отрезков, начиная с точки (0; 0; 0), имеют значения p, q и r, соответственно. Это можно проверить следующим образом: если положить, что координаты по оси y и z равны нулю, тогда x получается равен q. То есть точка пересечения с осью абсцисс имеет координаты (p; 0; 0). Аналогично рассуждая, получаем оставшиеся две координаты (0; q; 0) и (0; 0; r).

Уравнение параметрическое векторное

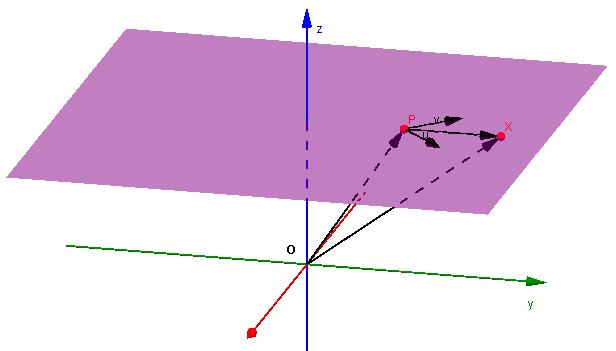
Это третий важный вид уравнения, который также часто используется при решении задач. Выше было показано, что плоскость однозначно задается точкой и нормальным вектором. Однако определить этот геометрический двумерный объект можно и иначе.

Предположим, что имеется два компланарных вектора, которые не параллельны друг другу. Обозначим их u¯(a₁; b₁; c₁) и v¯(a₂; b₂; c₂). Также известна точка Q(x₀; y₀; z₀). Каким будет уравнение плоскости, которая проходит через эту точку и два вектора?

Ответить на этот вопрос можно, получив уравнение в общем виде. Однако решим эту задачу другим способом. Вспомним, что любой вектор плоскости может быть разложен на два других компланарных вектора, которые также принадлежат этой плоскости. Это означает, что произвольный вектор QP¯, где P(x; y; z), может быть представлен в виде:

QP¯ = α*u¯ + β*v¯.

Пробегая все точки P плоскости, мы получим соответствующие параметры α и β. Приведенное для плоскости уравнение называется параметрическим векторным. Его записывают часто в координатном виде:

(x; y; z) = (x₀; y₀; z₀) + α*(a₁; b₁; c₁) + β*(a₂; b₂; c₂).

Видно, что эта форма записи плоскости аналогична векторному уравнению для прямой в двумерном и трехмерном случаях.

Это выражение также можно записать более явно, если разделить переменные:

x = x₀ + α*a₁ + β*a₂;
y = y₀ + α*b₁ + β*b₂;
z = z₀ + α*c₁ + β*c₂.

Эти три уравнения имеют форму аналогичную параметрическому уравнению для прямой в пространстве. Этот вид часто используется при преобразовании векторного уравнения в общее для плоскости.

Параллельные плоскости

Существует всего два варианта относительного положения двух плоскостей в пространстве. В этом пункте статьи приведем условие, когда они параллельны.

Если два уравнения плоскости даны в общем виде, то определить параллельность их достаточно просто. Две плоскости будут параллельны, если их вектора направляющие таковыми являются. Предположим, что имеются два уравнения:

A₁*x + B₁*y + C₁*z + D₁ = 0;
A₂*x + B₂*y + C₂*z + D₂ = 0.

Перпендикулярные к каждой из плоскостей вектора имеют координаты:

n₁¯ (A₁; B₁; C₁);
n₂¯ (A₂; B₂; C₂).

Если вектор n₁¯ можно представить в виде умножения на действительное число вектора n₂¯, тогда оба они будут параллельны, то есть:

n₂¯ = l*n₁¯, где l - действительное число.

Другой способ определения их параллельности заключается в нахождении косинуса угла между ними через скалярное произведение и модули векторов. Этот косинус должен быть равен единице, тогда вектора (плоскости) будут параллельными. Соответствующая формула имеет вид:

cos(φ) = |(n₁¯*n₂¯)|/(|n₁¯|*|n₂¯|) = 1.

Если же уравнения плоскостей в параметрической векторной форме даны, тогда параллельность в пространстве плоскостей также определяется из условия параллельности нормалей к ним. Чтобы найти направляющие вектора этих нормалей, следует взять векторные произведения образующих каждую плоскость векторов.

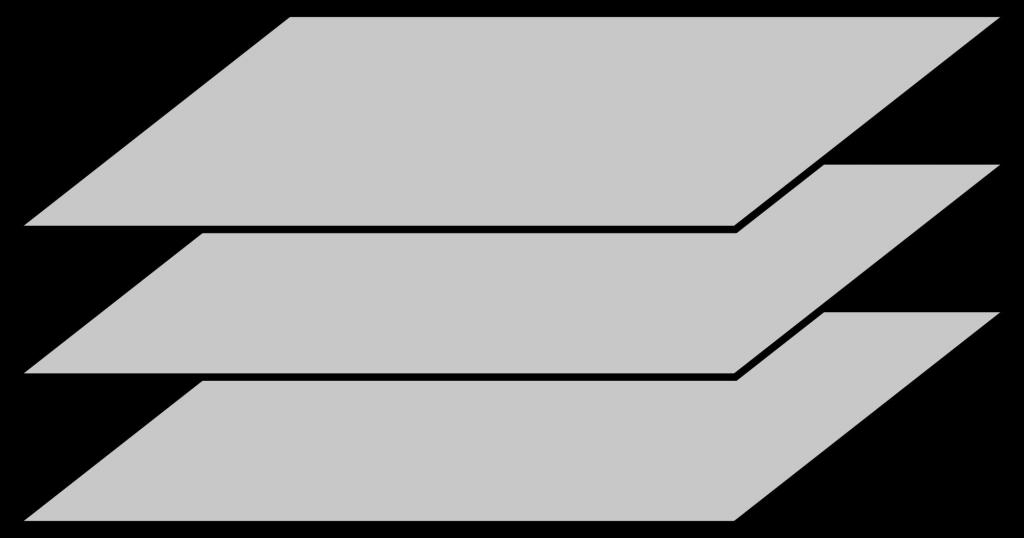
Рисунок выше показывает три плоскости, которые друг другу параллельны.

Пересечение плоскостей

Это второй вариант взаимного расположения в пространстве плоскостей. В этом случае две плоскости пересекаются по некоторой прямой, которая им принадлежит. В данном случае важно уметь рассчитывать двугранный угол этого пересечения. Он всегда равен углу между соответствующими направляющими векторами, то есть между перпендикулярами плоскостей.

В предыдущем пункте уже была приведена формула, позволяющая рассчитать угол между нормалями. Здесь лишь раскроем ее, записав через координаты векторов n₁¯ и n₂¯:

φ = arccos(|A₁*A₂+B₁*B₂+C₁*C₂|/(√(A₁²+B₁²+C₁²)*√(A₂²+B₂²+C₂²))).

Эта формула часто применяется при вычислении двугранных углов между плоскостями пирамиды или наклонной призмы.

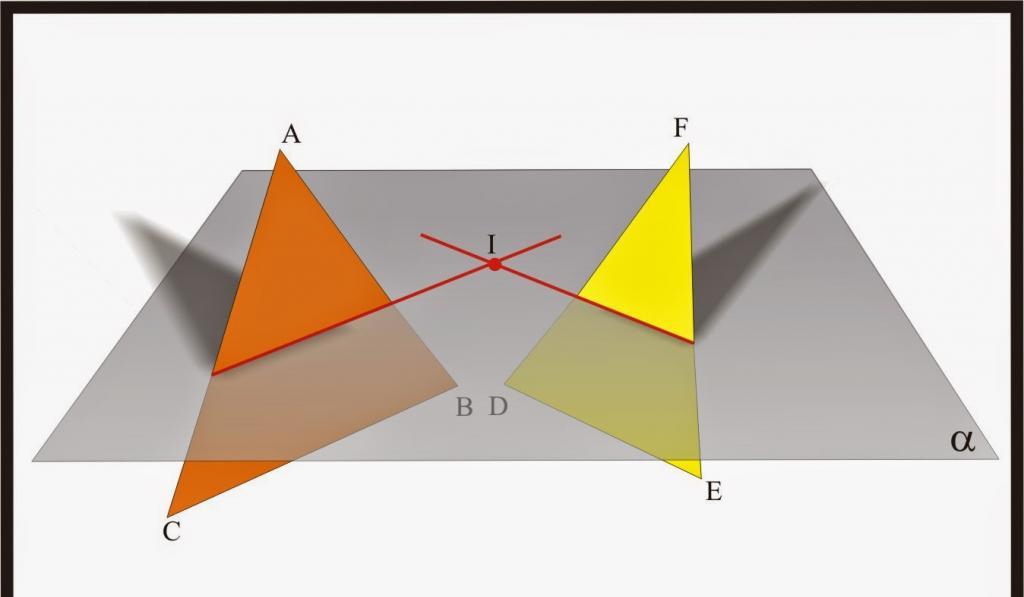
Две плоскости, которые пересекают третью горизонтальную, приведены на рисунке выше.

Частным случаем пересечения двух плоскостей является угол φ=90^o, то есть имеет место перпендикулярность рассматриваемых геометрических объектов. Для определения перпендикулярности не обязательно проводить расчеты угла φ по несколько громоздкой формуле выше, для этого будет достаточным рассчитать значение скалярного произведения n₁¯ и n₂¯. Для перпендикулярных плоскостей оно равно нулю, то есть:

(n₁¯*n₂¯) = A₁*A₂+B₁*B₂+C₁*C₂ = 0.

Пучок плоскостей

Если две плоскости пересекаются, то все общие их точки лежат на одной прямой. Отметим, что одним из методов задания прямой в пространстве является система двух общих уравнений плоскости. Сколько в пространстве плоскостей можно провести через одну прямую? Бесконечное число. Их совокупность называется пучком. Уравнение, которое описывает этот пучок, имеет следующую форму:

k₁*(A₁*x + B₁*y + C₁*z + D₁) + k₂*(A₂*x + B₂*y + C₂*z + D₂) = 0.

Здесь k₁ и k₂ являются произвольными числами. Частным случаем является ситуация, когда один или оба параметра k не могут принимать значение ноль. Предположим, что k₁≠0, тогда уравнение пучка можно перезаписать в виде:

(A₁*x + B₁*y + C₁*z + D₁) + k₂/k₁*(A₂*x + B₂*y + C₂*z + D₂) = 0.

Это равенство описывает все плоскости пучка кроме одной, имеющей направляющий вектор n₂¯(A₂; B₂; C₂).

Примером пучка плоскостей является совокупность листов отрытой книги.

Далее решим несколько геометрических задач, применяя полученные знания о свойствах плоскостей в пространстве.

Преобразование параметрического векторного уравнение в общее

Дано следующее плоскости уравнение в параметрическом векторной виде:

(x; y; z) = (1; 2; 0) + α*(1; 2; 3) + β*(-1; 3; 0).

Необходимо записать его в виде общего уравнения плоскости в пространстве.

Перепишем его в явном виде:

x = 1 + α - β;
y = 2 + 2*α + 3*β;
z = 3*α.

Из последнего выражения получаем α, затем подставляем его в первое равенство и выражаем β. Найденные параметры подставляем во второе уравнение, имеем:

α = z/3;
β = 1 - x + z/3;
y = 2 + 2*z/3 + 3 - 3*x + z =>
y + 3*x +5/3*z - 5 = 0 =>
9*x + 3*y + 5*z -15 = 0.

Таким образом, чтобы получить общее уравнение из векторного параметрического, следует сначала записать его в явном виде, а затем выразить параметры через переменные координаты.

Преобразование общего в параметрическое векторное уравнение

Эта задача является полностью противоположной предыдущей. Рассмотрим приемы, позволяющие ее решить.

Дано следующее уравнение:

x-2*y+3*z -1 = 0.

Для начала следует выразить одну координату через две другие. Выразим для примера x:

x=2*y-3*z +1.

Это означает, что плоскости будет принадлежать любая точка, имеющая координаты:

(2*y-3*z +1; y; z).

Теперь перепишем эту координату в виде суммы трех векторов, причем первый будет содержать только переменную y, второй - только z, а третий будет состоять исключительно из чисел. Имеем:

(x; y; z) = (2*y; y; 0) + (-3*z; 0; z) +(1; 0; 0).

Видно, что, раскрыв это уравнение, мы получим общие координаты для точки плоскости. Теперь остается только вынести за скобки переменные в первом и втором векторах и переобозначить их параметрами α и β. Получаем:

(x; y; z) = (1; 0; 0) + α*(2; 1; 0) + β*(-3; 0; 1).

Мы получили уравнение в параметрическом векторном виде, аналогичное исходному.

Изображение плоскости в системе координат

Задача заключается в следующем: по известному уравнению следует изобразить плоскость в пространстве. Соответствующее уравнение имеет вид:

3*x - y -4*z +5 = 0.

Чтобы изобразить эту плоскость, необходимо найти точки, в которых она пересекает оси координат. Для этого можно получить соответствующее уравнение в отрезках. Однако в данном случае поступим иначе: положим две координаты равными нулю и вычислим третью. Имеем:

y = 0; z = 0; x = -5/3;
x = 0; z = 0; y = 5;
x = 0; y = 0; z = 5/4.

Остается нанести полученные точки на оси координат и провести через них плоскость. Положение плоскости в пространстве изображено на рисунке ниже.

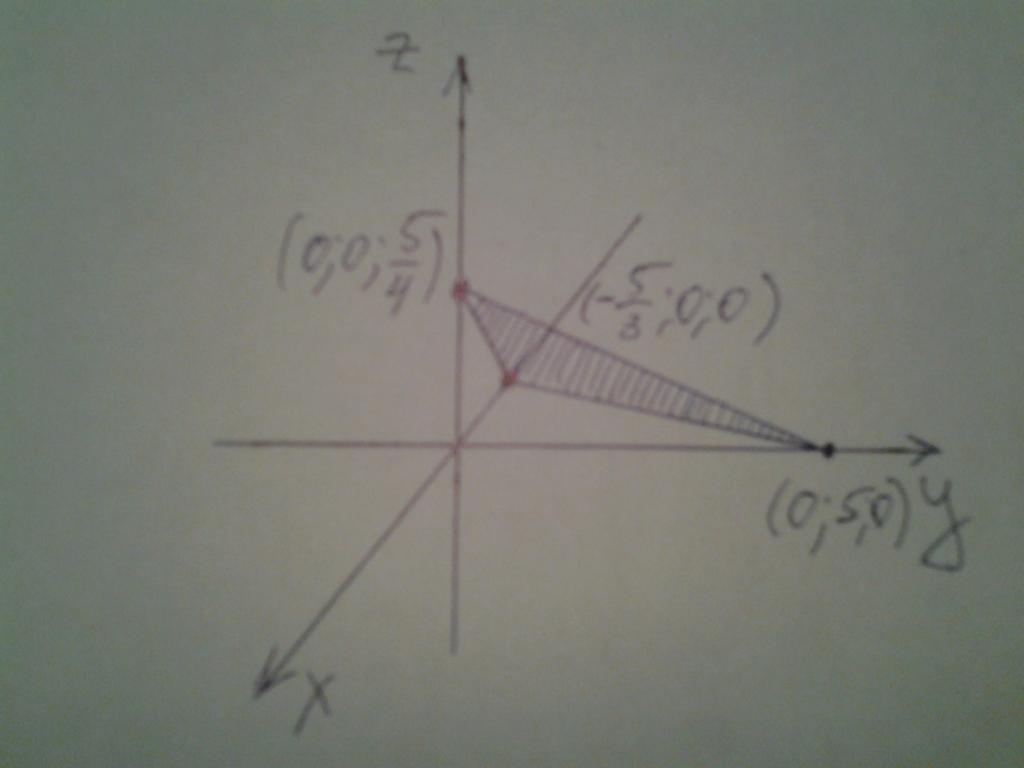
Три точки и плоскость

Пусть даны три точки в пространстве:

M(1; -1; 3);
N(3; 2; -4);
L(2; 5; 0).

Необходимо найти плоскость, которая через них проходит.

Из геометрии известно, что три точки, не лежащие на одной прямой, однозначно определяют плоскость. Ее уравнение можно составить, если найти ее вектор направляющий n¯. Он будет равен векторному произведению копланарных векторов, лежащих в плоскости. Координаты векторов можно получить из координат точек, например: