Свободные колебания. Общие сведения

В этой статье мы поговорим про свободные колебания. Рассмотрим их примеры: математический и пружинный маятники, а также колебательный контур.

Механические колебания

Колебательным движением, или механическими колебаниями называется движение тел или изменение состояния, которое повторяется со временем. Примерами в механике могут быть колебания маятников, струн, балансиров часов, мембран громкоговорителей, мостов и других сооружений.

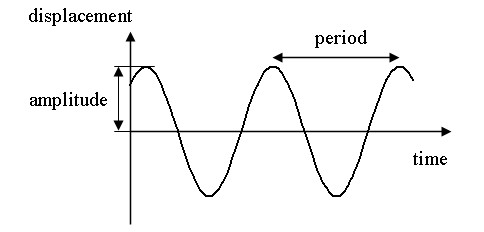
Периодическим называют колебательное движение, если значения физических величин, которые меняются во время колебаний, повторяются через одинаковые интервалы времени.

Минимальный интервал (промежуток) времени, через который повторяется положение тела во время колебательного движения, называют периодом колебания Т. Число колебаний, которые осуществляет тело за единицу времени, называют частотой колебаний ν.

Гармонические

Среди различных колебательных движений важное значение имеют гармонические колебательные движения.

Гармоническим называют колебание, во время которого материальная точка отклоняется от положения равновесия по закону синуса или косинуса.

Важность этого движения заключается в том, что многие колебательные движения в природе близки к гармоническим, а также потому, что сложные колебания можно разложить на гармонические. Запишем смещение материальной точки при гармоническом движении:

x = Asin(ωt + φ₀)

Буквой "x" обозначено отклонение точки, которая совершает колебания, от положения равновесия. Максимальное смещение от положения равновесия называют амплитудой. В нашем случае x_max = A. Аргумент (ωt + φ₀) называют фазой колебания, а величину φ₀ - начальной фазой колебания. Фаза позволяет определить смещение точки в определенный момент времени.

Период гармонического колебания T, учитывая то, что за период колебания фаза изменится на 2π, можно вычислить по формуле:

T = 2π/ω.

Частота свободных колебаний равна:

ν = 1/T = ω/2π.

Скорость точки при гармонических колебаниях находим как первую производную от смещения по времени:

v = dx/dt = Aωcos(ωt + φ₀).

Ускорение точки при гармонических колебаниях находим как вторую производную от смещения по времени:

a = dv/dt = Aω²cos(ωt + φ₀).

Свободные

Если в колебательной системе тело вывести из состояния равновесия и отпустить, то оно будет осуществлять так называемые свободные колебания, которые являются всегда затухающими.

Для исследования колебаний различной природы часто используют приборы, получившие название осциллографов. Осциллограф (от лат. oscillo - "колеблюсь" и греч. graph - "пишу") - прибор для наблюдения колебаний и их записи в графической форме.

Амплитуда колебаний в реальных системах со временем уменьшается, и колебания, в конце концов, прекращаются, поэтому свободные колебания являются всегда затухающими.

Период колебаний не зависит от их амплитуды, потому что в реальных механических системах всегда есть потери механической энергии.

Исследуя свободные колебания в системе "груз-пружина", при отсутствии потерь механической энергии, можно придти к выводу, что период таких колебаний определяется по формуле:

T = 2π/ω,

где ω - циклическая частота.

Частота свободных колебаний, соответственно, измеряется по формуле:

ν = 1/T = ω/2π.

Математический маятник

Математическим маятником считают точечное тело, подвешенное к нерастяжимой и невесомой нити. Математический маятник - это понятие абстрактное, потому что, во-первых, в природе не существует точечных тел, во-вторых, нет абсолютно нерастяжимых и невесомых нитей. Однако с определенным приближением математическим маятником можно считать шарик, подвешенный на нити. Когда шарик находится в состоянии равновесия, то на него действуют сила тяжести и сила упругости нити, которые уравновешивают друг друга, другими словами, равнодействующая этих сил равна нулю.

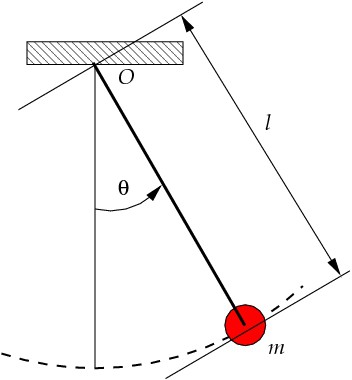
Период колебаний математического маятника можно вычислить по формуле:

T = 2π/ω,

где циклическая частота свободных колебаний ω² = l/g, а l - длина нитки.

Согласно формуле, можно сделать вывод, что период колебаний математического маятника не зависит от массы тела, а определяется только длиной подвеса и ускорением свободного падения.

Пружинный маятник

Еще одним примером гармонического свободного колебания являются колебания тела на пружине. В состоянии равновесия пружина пока не деформирована, сила упругости на тело не действует. Сила трения между телом и опорой также равна нулю. Сила притяжения уравновешена силой реакции опоры. Если вывести тело из состояния равновесия, переместив его вдоль оси OX на расстояние x = ± A, а затем отпустить, то маятник будет свободно колебаться под действием силы упругости, и свободные колебания маятника будут происходить по закону x = Asinwt.

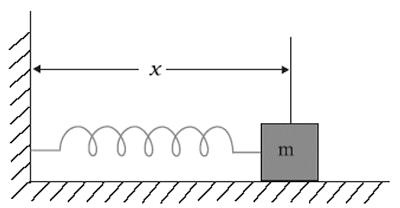
Период свободных колебаний маятника на пружине равен:

T = 2π/ω,

где циклическая частота колебаний ω² = k/m, k - жесткость пружины, m - масса тела.

Как видно из формулы, период и частота колебаний пружинного маятника не зависят от ускорения свободного падения, а определяются только массой подвешенного тела и жесткостью пружины.

Электрические колебания в контуре

Электрическая цепь, в которой возможны свободные электромагнитные колебания, называется колебательным контуром. Он складывается из конденсатора емкостью С, катушки с индуктивностью L и резистора с сопротивлением R (в реальном техническом контуре роль резистора играет сопротивление катушки и соединительных проводников).

Закон Ома для замкнутой цепи, которая не содержит внешнего источника тока, и в которой происходят свободные электромагнитные колебания, записывается в таком виде:

JR + U = - L(dJ/dt),

где U = q/C - напряжение на конденсаторе, q - заряд конденсатора, J = dq/dt - ток в цепи.

Свободные колебания в контуре - гармонические, поэтому меняются по следующему закону:

q(t) = q₀cos(ωt + φ₀).