Что такое консервативные силы? Потенциальные консервативные силы

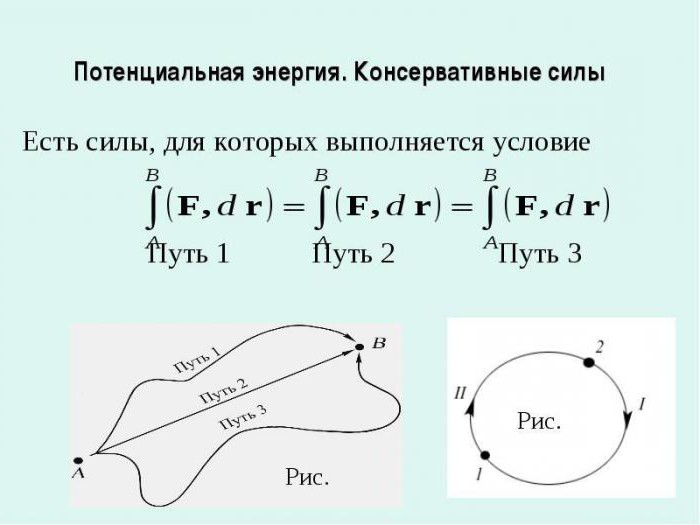
В механике используют такие силы, работа которых в случае перемещения тела по закрытому контуру равна нулю. Они называются потенциальные или консервативные силы.

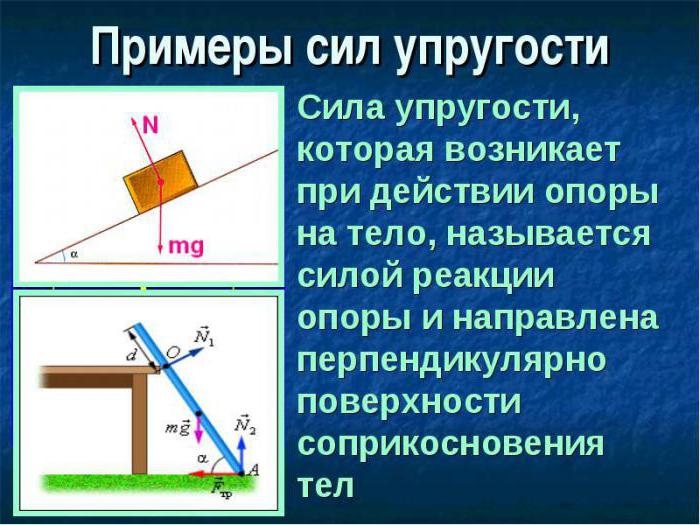
Свойства

У данных сил существуют два основных свойства:

• При переходе из одного положения в другое работа такой силы не связана с траекторией движения. Она связана только с конечным и начальным положениями имеющегося тела.
• В случае изменения направления перехода работа таких сил меняет знак, сохраняя свою величину.

Учитывая закон Гука и закон всемирного тяготения, можно подтвердить, что и сила упругости, и сила тяжести - это потенциальные (консервативные) силы.

Особенности

Потенциальность сил определяется тем, что в случае замкнутой траектории, во время совершения положительной работы на одном фрагменте, на втором участке совершается отрицательная работа, в итоге в сумме они дают ноль.

Примеры неконсервативных сил

Консервативными силами являются далеко не все силы, существующие в природе. К примеру, сила трения такой не является, она направлена во всех ситуациях против движения тела, на всем пути ее работа является отрицательной величиной. Рассчитывать работу консервативной силы можно благодаря уменьшению потенциальной величины.

En – потенциальная энергия тела, которая представляет собой скалярную величину. Она равна работе, которую совершают консервативные силы, переходя из исходного положения тела на нужный уровень отсчета.

Учитывая данное определение, можно записать формулу разности работ и энергий тела. В итоге можно говорить о том, что работа такой силы будет равна уменьшению потенциальной энергии.

Потенциальная гравитационная энергия

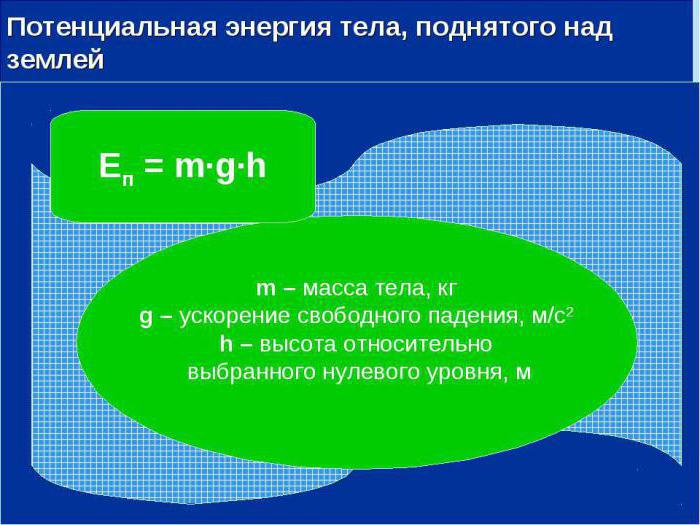
Если нужно определить потенциальную энергию тела, которое находится на некоторой высоте над поверхностью Земли, взять за начальный уровень отсчета можно любой горизонтальный уровень. Зная, что представляют собой консервативные силы, потенциальная энергия рассчитывается как работа, совершаемая силой тяготения в момент перехода тела с высоты на начало отсчета En = m·g·h.

Потенциальная энергия упругого тела

Есть и еще один вариант потенциальной энергии, который взаимосвязан с упругим взаимодействием молекул при незначительных деформациях твердых тел. Если взять в качестве примера сжатую пружину, возвращаемую в исходное состояние с помощью руки, то с ее стороны действует сила упругости, которая совершает работу.

Возьмем за начальную точку отсчета недеформированное (исходное) состояние пружины, тогда для вычисления работы силы упругости используем консервативные силы. Согласно закону Гука, сила упругости, которая действует на руку, будет пропорциональна деформации, направлена в сторону ее уменьшения. После того как пружина распрямляется, она перемещается на незначительный отрезок dx.

В таком случае ею совершается работа. Вычислить ее можно с помощью интеграла по закону Гука. Анализируя консервативные силы на этом примере, можно сделать вывод, что потенциальная энергия накапливается с целью последующего применения.

К тому же, если в случае кинетической энергии частицы (тела) применяется универсальное выражение, то при вычислении потенциальной обязательно учитывают все действующие на тело силы. Она всегда взаимосвязана с силой, которая действует с одной стороны тела на другое тело. К примеру, силой тяжести Земля воздействует на предмет, который падает с некоторой высоты, на шарик действует сжатая пружина, на стрелу влияет натянутая тетива.

Потенциальная энергия не присуща самому телу, она подразумевает взаимодействие тел, также действие друг на друга отдельных фрагментов одного тела. Рассмотрим ситуацию, когда во время движения тела, работу совершают лишь консервативные силы. Примеры таких случаев: падение с высоты, растяжение пружины.

Сумма потенциальной и кинетической энергии в рассматриваемой ситуации будет постоянной величиной, которую в механике принято называть полной механической энергией движущегося (покоящегося) тела.

Закон сохранения энергии

При наличии в системе только консервативных сил, не меняется полная механическая энергия всех сил, которые действуют в данной системе. Из этого можно сделать вывод, что для любых значений времени, величины полных механических энергий одинаковы. То есть: E2 = E1.

У закона сохранения механической энергии довольно ограниченный характер. Он не говорит о том, что происходит (в любом случае) сохранение механической энергии, а только указывает на условие, при котором это возможно, а именно при совершении работы консервативными силами.

В подобной ситуации происходит постоянный переход потенциальной энергии в кинетическую величину, затем обратный процесс. Если же на рассматриваемое тело действуют не консервативные силы, совершающие работу, то не наблюдается сохранение полной механической энергии.

Варианты действия сил

Допустим, что с некоторой высоты падает с нулевой начальной скоростью тело, силу сопротивления воздуха будем считать равной нулю. В таком случае на тело будет действовать лишь сила тяжести, являющаяся консервативной силой. В подобном примере выполняется в полной мере закон сохранения энергии.

В самом начале движения у тела есть только потенциальная энергия, определить которую можно по формуле: El = mgh. По мере падения тела происходит снижение величины потенциальной энергии, возрастание кинетической величины. При нулевой высоте тело получает максимальную скорость движения, и у него преобладает именно кинетическая энергия. Если внести величины в закон сохранения полной механической энергии, получим постоянную величину. В промежуточных участках у тела есть два вида внутренней энергии, но их суммарный показатель остается неизменной величиной.

В естествознании считают, что тела взаимодействуют между собой посредством полей. Под полем подразумевают ту область пространства, где в каждой точке есть сила, равномерно распределяемая между отдельными точками. В качестве типичного примера подобной силы вполне можно рассматривать классическую силу тяжести.