Формула Циолковского: использование и пример

Формула Константина Эдуардовича Циолковского выражает максимальную скорость летательного аппарата, которой он достигает во время полета при реактивном движении. Она получается при интегрировании уравнения Мещерского.

Формула Циолковского

Эта формула выражает скорость ракеты, переданную газами от сожженного топлива. Уравнение Мещерского и формула Циолковского неразрывно связаны - уравнение Мещерского описывает массу материальной точки, которая изменяется со временем, в то время как при реактивном движении ракеты постоянно идет уменьшение ее массы из-за сгорания топлива. Изменение скорости при изменяющейся массе (уменьшающейся в нашем случае) движущегося тела - вот что подразумевает под собой реактивное движение. Формула Циолковского основывается именно на нем.

Для решения ряда задач теоретической механики в области реактивного движения используют уравнение Мещерского (основное уравнение материальной точки переменной массы) и формулу Циолковского (формула конечной скорости летательного аппарата), которые называются основными соотношениям теории реактивного движения.

Основой при проектировании и планировании в области космических полетов является именно формула Циолковского, вывод которой стал настоящим прорывом для освоения космоса.

Задачи Циолковского

Для того, чтобы разрешить проблему межпланетных перелетов, К. Э. Циолковский рассмотрел в качестве средства перелета ракету. Он вывел формулу, с помощью которой можно получить зависимость массы летательного аппарата с топливом и скорости отдаления продуктов сгорания используемого топлива ракеты относительно нее. Покажем две его задачи:

• Исследование движения тела с переменной массы с действующей на него одной реактивной силы.
• Исследование движение тела в однородном поле силы тяжести переменной массы вблизи поверхности Земли.

Предисловие

Для всех космических полетов изначальной и основополагающей стала формула Циолковского для скорости ракеты, вывод которой представлен ниже.

Для начала необходимо приняв ее, грубо говоря, за материальную точку. На нее будут действовать силы притяжения Земли и других небесных тел (в момент взлета сила гравитации Земли будет, конечно же, наиболее сильной), сила сопротивления воздуха с одной стороны и противоположно им направленная реактивная сила, возникающая из-за выброса сгоревшего газа у основания тела. Ракета с большой силой выбрасывает эти газы, которые сообщают ей ускорение, направленное противоположно стороне выброса. Теперь необходимо представить эти рассуждения в виде формулы.

Сам принцип полета ракеты достаточно простой. С большой скоростью из ракеты вырывается газ, полученный при сгорании топлива, который сообщает самой ракете определенную силу, которая действует противоположно направлению движения. Так как считается, что внешние силы не действуют на ракету, то система будет замкнутой, и импульс ее не зависит от времени.

Уравнение Мещерского

Одним из основных примеров движения тела с изменяющейся массой является ракета с одной ступень, масса которой изменяется только из-за сжигания топлива, содержащегося в ней. Масса такой ракеты складывается из неизменяющейся (сама ракета и ее полезная нагрузка) и изменяющейся (топливо). Такой пример является упрощенной моделью.

Однако в современном ракетостроении используются многоступенчатые ракеты. Принцип их работы заключается в том, что благодаря большому объему ступеней они способны перевозить и использовать после взлета гораздо большее количество топлива. После его сгорания, ракете сообщается значительный импульс (гораздо больший, чем тот, которого можно добиться, используя одну ступень), а ставшие ненужными части открепляются от основы, уменьшая общий вес на 80-90%. Тем не менее, для расчета параметров многоступенчатой ракеты необходимо сложить показатели каждой из ее составляющей.

Дифференциальное уравнение Мещерского описывает движение материальной точки с переменной массой.

(m+dm)(υ+dυ) + dm′ υ′ - mυ = Fdt - в момент времени dt (разность между силой в момент времени t и dt+t и будет приращением).

Где m и υ зависят от времени, dt - какое-то время полета. За его образуется сила перемещения газа - dm′ υ′, dm′ - масса образованного из топлива газа. F - равнодействующая сила.

В описанном выше выражении приращения массы ракеты и газа и скорости устремляется к нулю, поэтому выражение принимает следующий вид:

mdυ = υ′′dm + Fdt,

причем υ′′ равняется разности скорости газа и скорости и является скоростью истечения газа.

- уравнение по форме начинает совпадать со вторым законом Ньютона - F = ma = m

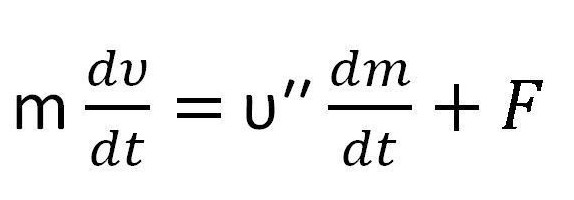
Оно и называется уравнением Мещерского.

Вывод формулы Циолковского

Необходимо вывести формулу, описывающую движение тела с переменной массой. Формула Циолковского таковой и является. Вывод представлен ниже.

В данных вычислениях считается, что на движущееся тело не действуют внешние силы, то есть F = 0.

Тогда mdυ = υ′′dm

Так как воздействие внешних сил на летящую ракету равно нулю, то она движется прямолинейно, а скорость движения противоположно направлена скорости выхода газа. Соответственно, υ = -υ′′

Получается выражение, которое необходимо проинтегрировать.

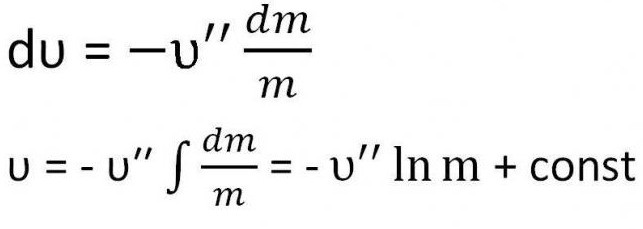
Необходимо найти константу. Для этого достаточно подставить в уравнение начальные условия - скорость равна нулю, а масса - сумме массы топлива и массы ракеты (m₀ + m)

Вообще говоря, m в формуле складывается из двух параметров - из полезной нагрузки и конструкции ракеты. Полезной нагрузкой называется общая масса груза и экипажа.

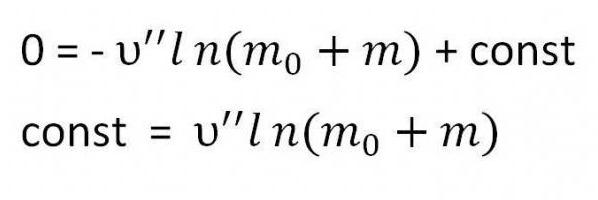
Подставляем найденную константу в формулу. В результате и получается выражение искомой формулы.

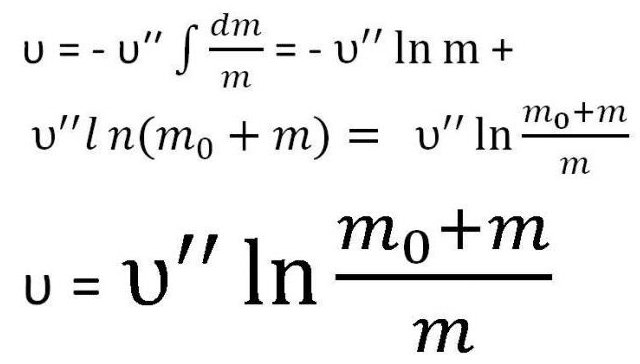
Это и есть один из вариантов формулы Циолковского для скорости. Однако иногда необходимо принять во внимание именно массу. Поэтому ее иногда записывают следующим образом:

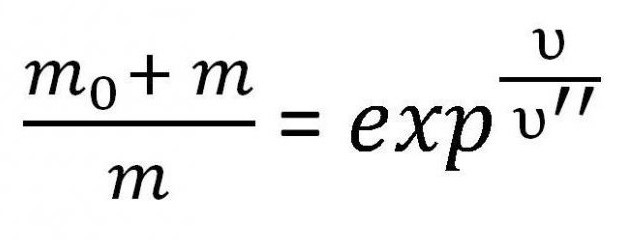
Данная формула используется для расчета массы топлива, которая требуется для развития определенной скорости при заданных условиях.

Рассмотрю далее небольшую задачу. Предположим, ракете необходимо развить первую космическую скорость для вращения по орбите Земли. Тогда для этого необходимо в первую очередь рассчитать массу топлива, конечно же. Тогда ее очень просто выразить из формулы Циолковского.

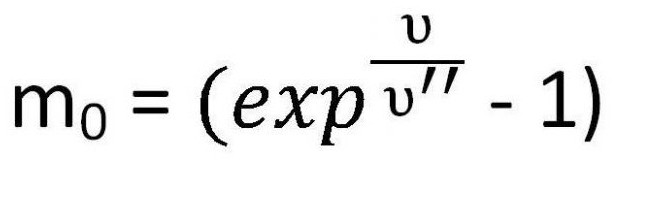
Релятивистская механика

Все вышеописанные формулы могут применяться только в том случае, когда скорость ракеты много меньше скорости света (υ<<c), потому что тогда возможно использование нерелятивистских законов механики.

Однако если скорость движения ракеты можно сравнить со скоростью света, то необходимо применять уже другие законы.

Пусть m и υ - масса ракеты в состояние и ее скорость в любое время t, а υ′ и m′ - скорость выхода газа и его масса в это же время. То есть m′ - масса вышедшего газа, поэтому его значение для расчета неважно, m′ = 0.

Необходимо расписать закон сохранения импульса и закон сохранения энергии в релятивистской механике, затем продифференцировать первое уравнение, учитывая, что m′=0 и получить выражение третье.

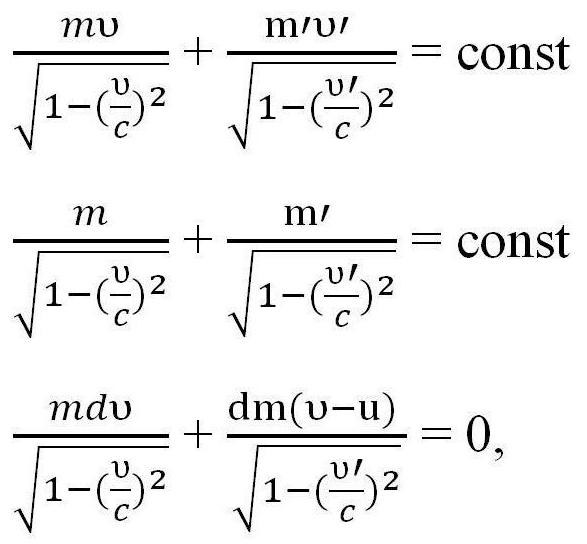
где u - скорость испускания газов.

Исходя из закона сложения скоростей в релятивистской, механике следует такое выражение. Его необходимо преобразовать относительно υ′ и проинтегрировать для получения окончательного варианта уравнения.

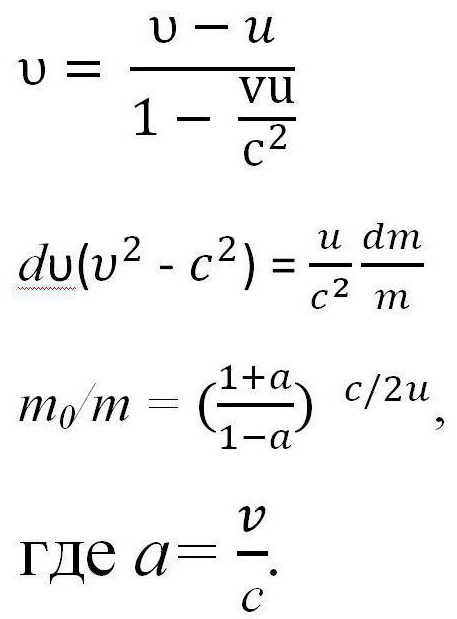
И далее получается формула Циолковского для скорости, сравнимой со скоростью света. Также ее можно назвать релятивистской формулой Циолковского.

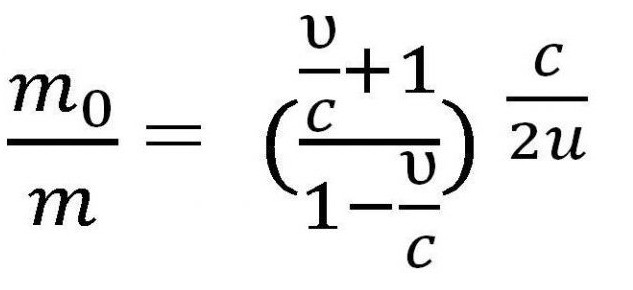
Можно несколько усложнить задачу и рассмотреть в качестве примера ракету с несколькими ступенями. Таким образом, формула Циолковского для многоступенчатой ракеты представляет собой сумму необходимых для расчета параметров. То есть, для того, чтобы рассчитать скорость для многоступенчатой ракеты, следует сложить скорость каждой из составляющей части.

Несколько выводов из формулы Циолковского

Основа всех космических полетов - формула Циолковского.

• Скорость движения непосредственно зависит от относительной скорости выбрасывания газов, поэтому, чем больше скорость выбрасывания, тем быстрее летит ракета.
• Чем больше отношение суммы массы ракеты и массы топлива к массе ракеты, тем больше скорость ракеты. Увеличение происходит даже по определенной зависимости - если отношение масс увеличивается в геометрической прогрессии, то есть, каждое предыдущее число меньше последующего в определенное количество раз, то скорость растет в арифметической прогрессии - каждое предыдущее число меньше последующего на определенное число. Однако это совершенно не означает, что скорость пропорциональна массе. Сам Циолковский в своих трудах замечал, что скорость растет медленнее по сравнению с увеличением топлива, однако не имеет предела.
• Соответственно, для развития больше скорости необходимо увеличивать скорость выбрасывания газа и массу топлива.

КПД ракеты

При расчете полета важно четко осознавать, какой именно процент полученной после сгорания топлива энергии используется в качестве полезной работы?

Таким образом, коэффициентом полезного действия принято называть отношение кинетических энергий ракеты и газов после выбрасывания. Обозначим m и m′ за массу ракеты в начале и в конце полета, продолжающийся время t. Соответственно, - скорость выбрасывания газов.

Тогда, по формуле Циолковского, КПД двигателя ракеты можно найти следующим образом:

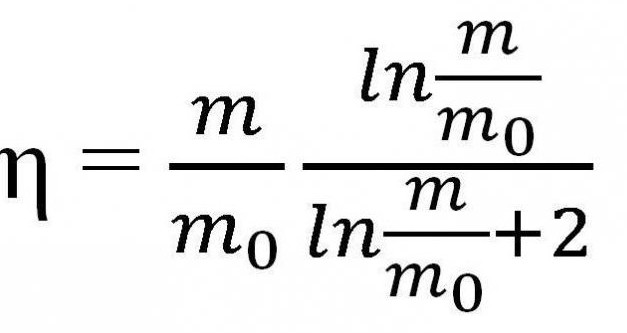
Следует заметить, что данный КПД является очень небольшим и не превышает 5%, притом как у тепловых двигателей этот показатель равняется и 80%.

Другая форма формулы

В некоторых ресурсах применяется несколько иная формула Циолковского, уравнение, в котором вместо υ′ применяется другой параметр - I. В данном случае I называют удельным импульсом, и даже приводится объяснение, что удельный импульс выражается через тягу двигателя и его сжиганию массы топлива за единицу времени. Первый вопрос, который приходит на ум - вопрос о размерности. В отличие от скорости, импульс имеет другую размерность, которая будет противоречить сути формулы. Однако, непосредственно удельный импульс совпадает по размерности со скоростью.

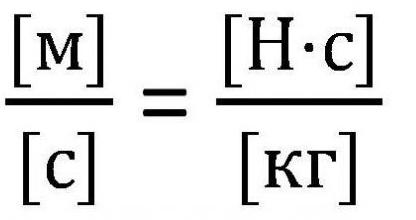
Удельный импульс показывает количество секунд, при котором двигатель, истратив единицу топлива, получит единицу силы. Применяется сугубо в описании реактивного двигателя.

Использование при создании ракет

Формулу Циолковского для многоступенчатой ракеты применяют и при проектировании ракеты. Для этого используется совершенно логичная зависимость, которая практически является прямопропорциональной - чем больше используется при полете топлива, тем больше будет масса самой ракеты. Это обуславливается тем, что для перевозки большого количества топлива требуются, соответственно, и большие резервуары, поэтому увеличивается в результате и размер корабля, и даже сам двигатель. Некоторым решением возникающей проблемы является использование твердого топлива, которое требует меньше условий для хранения. Однако в настоящий момент оно обладает наименьшим удельным импульсом из существующих.

Космические скорости

Формула Циолковского используется также для расчета необходимого количества топлива для развития определенной скорости - обычно это одна из четырех космических.

• Первая космическая скорость - корабль выходит на орбиту планеты. Для Земли равняется примерно 7.91 км/с.
• Вторая космическая скорость - ракета преодолевает силу притяжения и выходит в открытое пространство. Для Земли - 11.2 км/с.
• Третья космическая скорость - ракета преодолевает силу притяжения звезды в системе (например, Солнца) и выходит за пределы. Для Солнечной системы - 42 км/с, однако эти расчеты являются неточными из-за необходимости преодолевать притяжение планеты.
• Четвертая космическая скорость - корабль способен покинуть Галактику. Для Млечного пути - более 500 км/с, рассчитывается в зависимости от точки нахождения.