Импульс тела: определение и свойства

В повседневной жизни для того, чтобы охарактеризовать человека, совершающего спонтанные поступки, иногда используют эпитет «импульсивный». При этом некоторые люди даже не помнят, а значительная часть и вовсе не знает, с какой физической величиной связано это слово. Что скрывается под понятием «импульс тела» и какими свойствами он обладает? Ответы на эти вопросы искали такие великие ученые, как Рене Декарт и Исаак Ньютон.

Импульс тела: определение

Как и всякая наука, физика оперирует четко сформулированными понятиями. На данный момент принято следующее определение для величины, носящей название импульса тела: это векторная величина, которая является мерой (количеством) механического движения тела.

Предположим, что вопрос рассматривается в рамках классической механики, т. е. считается, что тело движется с обычной, а не с релятивистской скоростью, а значит, она хотя бы на порядок меньше скорости света в вакууме. Тогда модуль импульса тела рассчитывается по формуле 1 (см. фото ниже).

Таким образом, по определению, эта величина равна произведению массы тела на его скорость, с которой сонаправлен ее вектор.

В качестве единицы измерения импульса в СИ (Международной системе единиц) принимается 1 кг/м/с.

Откуда появился термин «импульс»

За несколько веков до того, как в физике появилось понятие количества механического движения тела, считалось, что причиной любого перемещения в пространстве является особая сила — импетус.

В 14 веке в это понятие внес коррективы Жан Буридан. Он предположил, что летящий булыжник обладает импетусом, прямо пропорциональным скорости, который был бы неизменным, если бы отсутствовало сопротивления воздуха. В то же время, по мнению этого философа, тела с большим весом обладали способностью «вмещать» больше такой движущей силы.

Дальнейшее развитие понятию, позднее названного импульсом, дал Рене Декарт, который обозначил его словами «количество движения». Однако он не учитывал, что скорость имеет направление. Именно поэтому выдвинутая им теория в некоторых случаях противоречила опыту и не нашла признания.

О том, что количество движения должно иметь еще и направление, первым догадался английский ученый Джон Валлис. Произошло это в 1668 году. Однако понадобилась еще пара лет, чтобы он сформулировал известный закон сохранения количества движения. Теоретическое доказательство этого факта, установленного эмпирическим путем, было дано Исааком Ньютоном, который использовал открытые им же третий и второй законы классической механики, названные его именем.

Импульс системы материальных точек

Рассмотрим сначала случай, когда речь идет о скоростях, намного меньших, чем скорость света. Тогда, согласно законам классической механики, полный импульс системы материальных точек представляет векторную величину. Он равен сумме произведений их масс на скорости (см. формулу 2 на картинке выше).

При этом за импульс одной материальной точки принимают векторную величину (формула 3), которая сонаправлена со скоростью частицы.

Если речь идет о теле конечного размера, то сначала его мысленно разбивают на малые части. Таким образом, снова рассматривается система материальных точек, однако ее импульс рассчитывают не обычным суммированием, а путем интегрирования (см. формулу 4).

Как видим, временная зависимость отсутствует, поэтому импульс системы, на которую не воздействуют внешние силы (или их влияние взаимно компенсировано), остается неизменным во времени.

Доказательство закона сохранения

Продолжим рассматривать тело конечного размера как систему материальных точек. Для каждой из них Второй закон Ньютона формулируется согласно формуле 5.

Обратим внимание на то, что система замкнутая. Тогда, суммируя по всем точкам и применяя Третий закон Ньютона, получаем выражение 6.

Таким образом, импульс замкнутой системы является постоянной величиной.

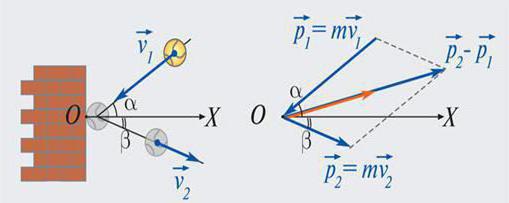
Закон сохранения справедлив и в тех случаях, когда полная сумма сил, которые действуют на на систему извне, равна нулю. Отсюда следует одно важное частное утверждение. Оно гласит, что импульс тела является постоянной величиной, если воздействие извне отсутствует или влияние нескольких сил скомпенсировано. Например, в отсутствие трения после удара клюшкой шайба должна сохранять свой импульс. Такая ситуация будет наблюдаться даже невзирая на то, что на это тело действуют сила тяжести и реакции опоры (льда), так как они, хотя и равны по модулю, однако направлены в противоположные стороны, т. е. компенсируют друг друга.

Свойства

Импульс тела или материальной точки является аддитивной величиной. Что это значит? Все просто: импульс механической системы материальных точек складывается из импульсов всех входящих в систему материальных точек.

Второе свойство этой величины заключается в том, что она остается неизменной при взаимодействиях, которые изменяют лишь механические характеристики системы.

Кроме того, импульс инвариантен по отношению к любому повороту системы отсчета.

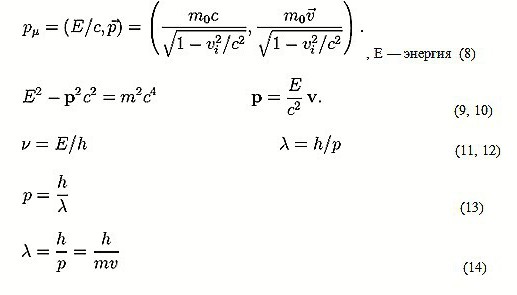
Релятивистский случай

Предположим, что речь идет о невзаимодействующих материальных точках, имеющих скорости порядка 10 в 8-й степени или чуть меньше в системе СИ. Трехмерный импульс рассчитывается по формуле 7, где под с понимают скорость света вакууме.

В случае, когда она замкнутая, верен закон сохранения количества движения. В то же время трехмерный импульс не является релятивистски инвариантной величиной, так как присутствует его зависимость от системы отсчета. Есть также четырехмерный вариант. Для одной материальной точки его определяют по формуле 8.

Импульс и энергия

Эти величины, а также масса тесно связаны друг с другом. В практических задачах обычно применяются соотношения (9) и (10).

Определение через волны де Бройля

В 1924 году была высказана гипотеза о том, что корпускулярно-волновым дуализмом обладают не только фотоны, но и любые другие частицы (протоны, электроны, атомы). Ее автором стал французский ученый Луи де Бройль. Если перевести эту гипотезу на язык математики, то можно утверждать, что с любой частицей, имеющей энергию и импульс, связана волна с частотой и длиной, выражаемыми формулами 11 и 12 соответственно (h — постоянная Планка).

Из последнего соотношения получаем, что модуль импульса и длина волны, обозначаемая буквой «лямбда», обратно пропорциональны друг другу (13).

Если рассматривается частица со сравнительно невысокой энергией, которая движется со скоростью, несоизмеримой со скоростью света, то модуль импульса вычисляется так же, как в классической механике (см. формулу 1). Следовательно, длина волны рассчитывается согласно выражению 14. Иными словами, она обратно пропорциональна произведению массы и скорости частицы, т. е. ее импульсу.

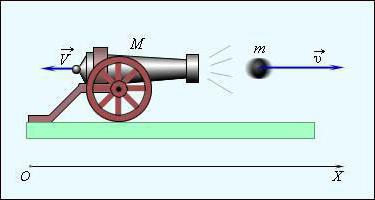
Теперь вы знаете, что импульс тела — это мера механического движения, и познакомились с его свойствами. Среди них в практическом плане особенно важен Закон сохранения. Даже люди, далекие от физики, наблюдают его в повседневной жизни. Например, всем известно, что огнестрельное оружие и артиллерийские орудия дают отдачу при стрельбе. Закон сохранения импульса наглядно демонстрирует и игра в бильярд. С его помощью можно предсказать направления разлета шаров после удара.

Закон нашел применение при расчетах, необходимых для изучения последствий возможных взрывов, в области создания реактивных аппаратов, при проектировании огнестрельного оружия и во многих других сферах жизни.