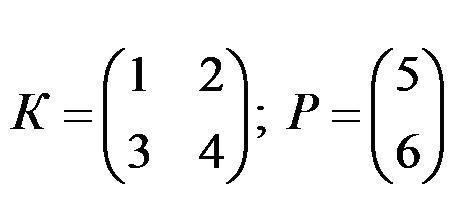Тип данных: массивы. Это просто и элегантно
В программировании зачастую приходится встречаться с таким типом данных, как массивы. Это наиболее простое решение при выполнении схожих операций с большим количеством однотипных переменных. Если пытаться написать программу, которая будет включать в себя все эти данные и повторяющиеся вычисления, то целесообразнее включить в продукт структуру, называемую массивом, или же матрицей.
Общее понятие о массивах
Под матрицей (некоторым проще представить ее в виде таблицы) понимается последовательность ячеек памяти, в которых хранятся однотипные переменные. При этом взаимосвязь между данными и структурой осуществляется через одно имя и указываемый индекс. Именно он помогает определить, какую переменную нужно использовать при решении задачи.

Следует четко понимать, что индекс отнюдь не является содержимым ячейки. Он лишь указывает на те данные, которые содержатся в конкретной ячейке.
Определение такой структуры будет звучать следующим образом: массивы – это группа однотипных данных, имеющая собственное имя и хранящая переменные в последовательных ячейках памяти.
Существует два вида матриц: одномерная (линейная) структура и двумерный массив. Первый тип представлен в виде таблицы, в которой всего одна строка или один столбец. В конкретном случае количество индексов показывает размер матрицы.
Двумерный массив – структура, представленная в виде таблицы, в которой номер строки указывает на первый индекс, а номер столбца – на второй. Так, в матрице А (m,n) элемент массива а23 показывает, что эта переменная находится на второй строке и в третьем столбце. Причем m задает количество строк, а n – число столбцов. Различают квадратную матрицу (где число строк и столбцов одинаково) и прямоугольную.
Массивы в программировании
Мы уже выяснили, что массивы – это набор однотипных элементов. Причем тип данных должен быть одинаковым во всей таблице. В каждой структуре может быть совершенно другой тип данных: числовой, строковый, символьный.
При написании программы задавать границы можно двумя способами:
- с использованием имени типа, где первое и последнее значение является ограничителем;
- с применением ранее объявленных констант.
Задавать структуру также можно несколькими способами. Хотелось бы заметить, что в каждом программном языке имеется свой синтаксис. Но принцип создания матрицы похож. В первом случае конкретный элемент вызывается с помощью имени переменной структуры и индекса, указываемого в квадратных скобках. В другом случае матрицу можно задать путем простого перечисления всех элементов.
Не нужно путать понятия «индекс» и «тип индекса». Первое определение указывается в разделе операторов с целью возможности обозначения конкретного элемента массива. А тип индекса используется только в разделе описания структуры. Размерность массива задается в описании. Крайне нежелательно менять количество элементов в процессе работы над программой.
Заполнять матрицы данными в программировании можно следующими способами:
- посредством ручного ввода с клавиатуры;
- с использованием генератора случайных чисел;
- при объявлении массива как константы;
- по заданной формуле.
Структуризация массива
Массивы – это структурированный тип данных. Как уже было сказано, матрица (если она двумерная) состоит из конечного числа строк и столбцов; если же она линейная - то из одной строки или одного столбца, где количество элементов также ограничено.
Пересечение строки и столбца называется ячейкой. В ней указываются конкретные переменные. Не допускается наличие различных типов данных в одной таблице. Элементы массива – это переменные с индексами (независимо от того, линейная это структура или двумерная). Индекс – это номер конкретной ячейки. Он указывает на ее положение в таблице.
Операции с массивами: сложение
Итак, массив данных что в математике, что в информатике, – набор переменных. С ним можно проводить различные операции: сложение, вычитание, транспонирование, умножение, деление.
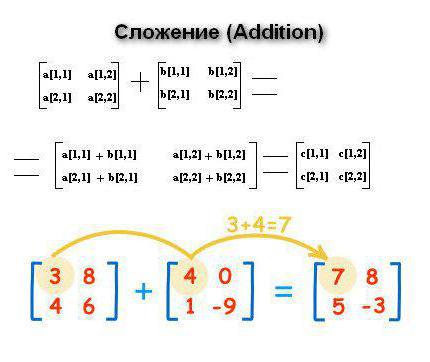
При сложении необходимо учитывать тот факт, что размерность обеих структур должна быть одинаковой. В таком случае, если заданы матрицы А и В с размерностью MxN, то в получившейся С=А+В элементами будут c[i,j]=a[i,j]+b[i,j]. Получается, что переменные складываются поэлементно.
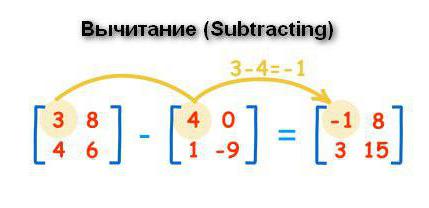
Операции с массивами: вычитание
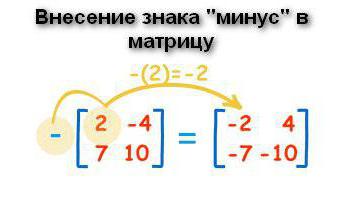
Этот пункт, пожалуй, следует начать с вынесения знака «минус» из матрицы (ну или, наоборот, внесения). Бывают случаи, когда массив данных состоит из элементов, в большинстве своем отрицательных. В такой ситуации предпочтительнее будет вынести минус за пределы структуры. Для этого перед таблицей ставится отрицательный знак, а у каждого элемента знак меняется на противоположный. Ноль в данном случае соблюдает нейтралитет: у него нет положительного или отрицательного знака.
Вычитание проводится по тому же принципу, что и сложение. Из элемента первой матрицы вычитается переменная с таким же индексом из другой структуры. Ответ записывается в третьей таблице на соответствующей позиции.
Операции с массивами: умножение и деление
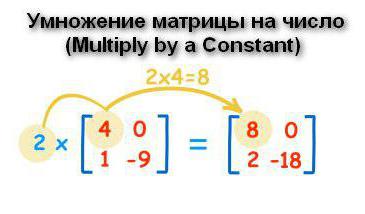
Кроме сложения и вычитания массив чисел можно умножать на число, перемножать две структуры между собой, делить одну на другую.
Чтобы найти произведение матрицы и числа, необходимо каждый элемент массива умножить на указанный элемент. Ответ записывается в ячейку с таким же индексом, как и первоначальная переменная.
- Количество столбцов первой таблицы равно числу строк второго множителя. В таком случае размерность полученной матрицы будет таковой: число строк будет равняться количеству строчек первого множителя, а количество столбцов будет равняться их числу из второго множителя.
- Рассмотрим два множителя.
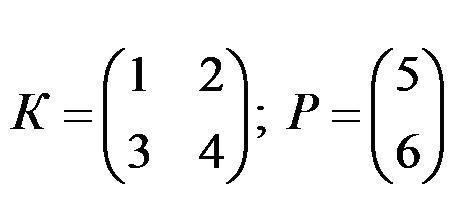
- Поскольку число столбцов во множителе К равняется количеству строк в массиве Р, тогда проведение операции возможно. Но если поменять матрицы местами, то закон о перемене мест множителей здесь не работает. Поэтому Р х К – неверная запись. Если обе матрицы квадратные, то проведение операции возможно в обоих случаях.
Формула умножения выглядит следующим образом.
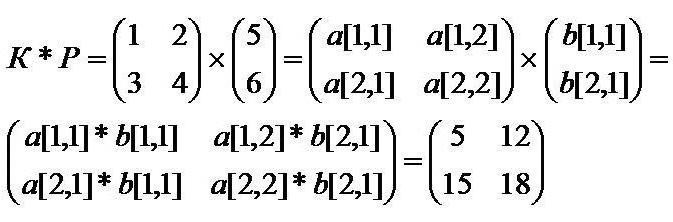
Если оба множителя двумерные, тогда следует придерживаться принципа, представленного на иллюстрации ниже.

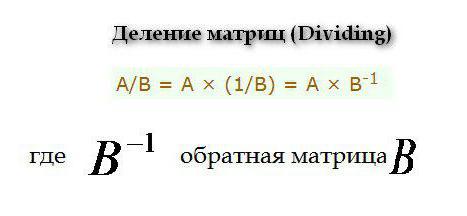

Транспонирование
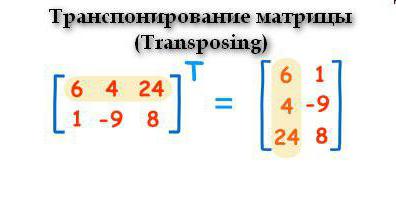
Данная операция проводится по следующему принципу: строки становятся столбцами. Выглядит это следующим образом.
Похожие статьи
- Выступающая надбровная дуга - о чем это говорит?
- JavaScript, массивы: описание
- Массивы JS. Объект JS. Многомерные массивы JavaScript
- PHP-массив: функции и значение
- Типы данных в "Си". Программирование на языке "Си"
- Быстрая сортировка - один из лучших методов сортировки массивов
- PHP массив в массиве: пример