Дискриминант: примеры решений. Как решать квадратные уравнения через дискриминант

Квадратные уравнения часто появляются во время решения различных задач физики и математики. В данной статье мы рассмотрим, как решать эти равенства универсальным способом "через дискриминант". Примеры использования полученных знаний также даются в статье.

О каких уравнениях пойдет речь?

На рисунке ниже изображена формула, в которой x - неизвестная переменная, а латинские символы a, b, c представляют собой некоторые известные числа.

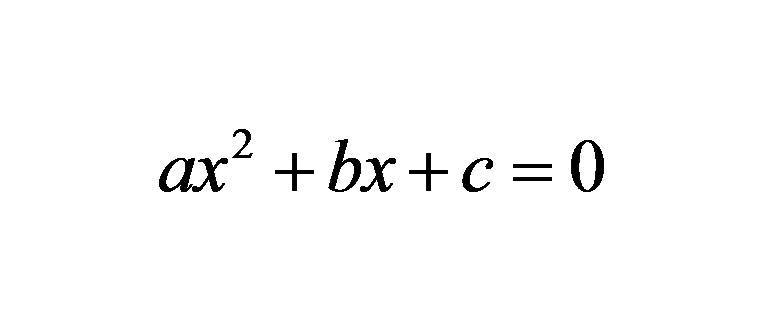
Каждый из этих символов называется коэффициентом. Как можно заметить, число "a" стоит перед переменной x, возведенной в квадрат. Это максимальная степень представленного выражения, поэтому оно называется квадратным уравнением. Часто используют другое его название: уравнение второго порядка. Само значение a - это квадратный коэффициент (стоящий при переменной в квадрате), b - это линейный коэффициент (он находится рядом с переменной, возведенной в первую степень), наконец, число c - свободный член.

Отметим, что вид уравнения, который изображен на рисунке выше, является общим классическим квадратным выражением. Помимо него существуют другие уравнения второго порядка, в которых коэффициенты b, c могут быть нулевыми.

Когда ставят задачу решить рассматриваемое равенство, то это означает, что такие значения переменной x нужно найти, которые бы ему удовлетворяли. Здесь первым делом нужно запомнить следующую вещь: поскольку максимальная степень икса - это 2, то данный тип выражений не может иметь больше, чем 2 решения. Это означает, что если при решении уравнения были найдены 2 значения x, которые ему удовлетворяют, то можно быть уверенным, что не существует никакого 3-го числа, подставляя которое вместо x, равенство также бы являлось истиной. Решения уравнения в математике называют его корнями.

Способы решения уравнений второго порядка

Решения уравнений этого типа требует знания некоторой теории о них. В школьном курсе алгебры рассматривают 4 различных метода решения. Перечислим их:

• с помощью факторизации;
• используя формулу для полного квадрата;
• применяя график соответствующей квадратичной функции;
• используя уравнение дискриминанта.

Плюс первого метода заключается в его простоте, однако, он не для всех уравнений может применяться. Второй способ является универсальным, однако несколько громоздким. Третий метод отличается своей наглядностью, но он не всегда удобен и применим. И, наконец, использование уравнения дискриминанта - это универсальный и достаточно простой способ нахождения корней абсолютно любого уравнения второго порядка. Поэтому в статье рассмотрим только его.

Формула для получения корней уравнения

Обратимся к общему виду квадратного уравнения. Запишем его: a*x²+ b*x + c =0. Перед тем как пользоваться способом его решения "через дискриминант", следует приводить равенство всегда к записанному виду. То есть оно должно состоять из трех слагаемых (или меньше, если b или c равен 0).

Например, если имеется выражение: x²-9*x+8 = -5*x+7*x², то сначала следует перенести все его члены в одну сторону равенства и сложить слагаемые, содержащие переменную x в одинаковых степенях.

В данном случае эта операция приведет к следующему выражению: -6*x²-4*x+8=0, которое эквивалентно уравнению 6*x²+4*x-8=0 (здесь левую и правую части равенства мы умножили на -1).

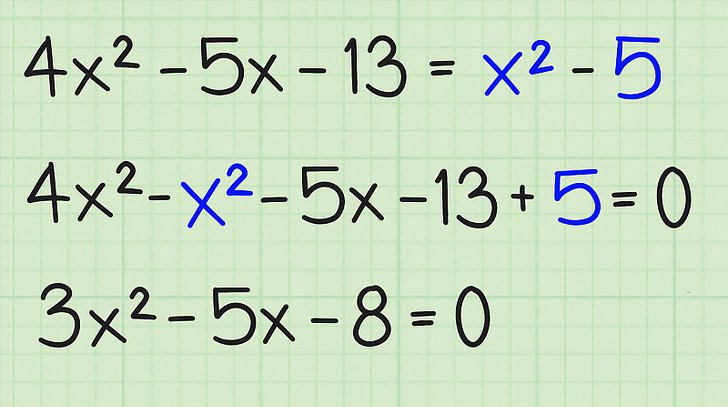
Как только усвоен описанный выше шаг, далее, следует научиться различать коэффициенты. Здесь все просто: при x² всегда стоит a, при x¹ находится b, свободный член c представляет собой не связанное с x число.

В примере выше a = 6, b=4, c=-8. Заметим, что все члены рассматриваемого равенства всегда суммируются между собой, поэтому если появляется знак "-", то это означает, что отрицательным является соответствующий коэффициент, как число c в данном случае.

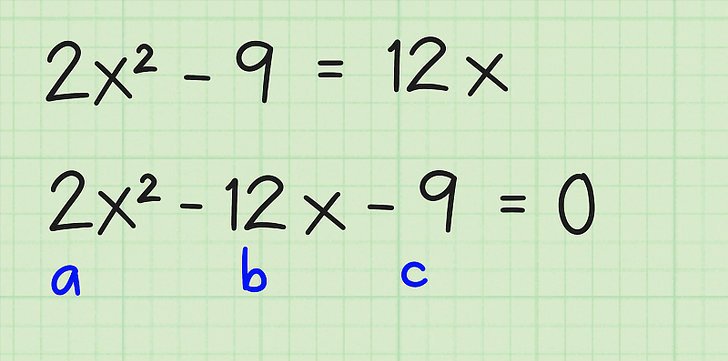
Разобрав этот момент, перейдем теперь к самой формуле, которая дает возможность получения корней квадратного уравнения. Она имеет вид, который представлен на фото ниже.

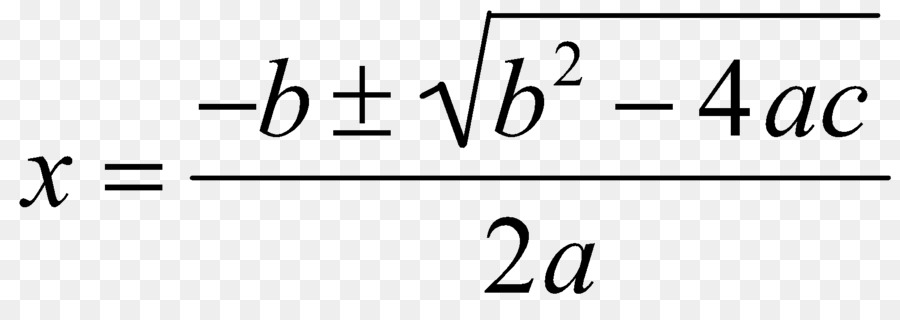
Как видно из этого выражения, оно позволяет получать два корня (следует обратить внимание на знак "±"). Для этого в него достаточно подставить коэффициенты b, c, и a.

Понятие о дискриминанте

В предыдущем пункте была приведена формула, которая позволяет быстро решить любое уравнение второго порядка. В ней подкоренное выражение называют дискриминантом, то есть D = b²-4*a*c.

Почему эту часть формулы выделяют, и она даже имеет собственное название? Дело в том, что дискриминант связывает в единое выражение все три коэффициента уравнения. Последний факт означает, что он полностью несет информацию о корнях, которую можно выразить следующим списком:

1. D>0: равенство имеет 2 различных решения, причем оба они представляют собой действительные числа.
2. D<0: также получаются два корня, но оба они комплексные. Этот тип выражений научились решать только в эпоху Возрождения, когда математиками нового времени было введено понятие "мнимая единица".
3. D=0: у уравнения всего один корень, и он является действительным числом.

Далее в статье приведены примеры с дискриминантом квадратных уравнений и дано их решение.

Задача на определение дискриминанта

Приведем простой пример, как найти дискриминант. Пусть дано такое равенство: 2*x² - 4+5*x-9*x² = 3*x-5*x²+7.

Приведем его к стандартному виду, получаем: (2*x²-9*x²+5*x²) + (5*x-3*x) + (- 4-7) = 0, откуда приходим к равенству: -2*x²+2*x-11 = 0. Здесь a=-2, b=2, c=-11.

Теперь можно воспользоваться названной формулой для дискриминанта: D = 2² - 4*(-2)*(-11) = -84. Полученное число является ответом на поставленную задачу. Поскольку в примере дискриминант меньше нуля, то можно сказать, что данное квадратное уравнение не имеет действительных корней. Его решением будут только числа комплексного типа.

Пример неравенства через дискриминант

Решим задачи несколько иного типа: дано равенство -3*x²-6*x+c = 0. Необходимо найти такие значения c, для которых D>0.

В данном случае известно лишь 2 из 3 коэффициентов, поэтому рассчитать точное значение дискриминанта не получится, однако известно, что он является положительным. Последний факт используем при составлении неравенства: D= (-6)²-4*(-3)*c>0 => 36+12*c>0. Решение полученного неравенства приводит к результату: c>-3.

Проверим полученное число. Для этого вычислим D для 2 случаев: c=-2 и c=-4. Число -2 удовлетворяет полученному результату (-2>-3), соответствующий дискриминант будет иметь значение: D = 12>0. В свою очередь, число -4 не удовлетворяет неравенству (-4<-3), вычисляем дискриминант: D = -12<0, что противоречит условию задачи.

Таким образом, любые числа c, которые больше -3, будут удовлетворять условию.

Пример решения уравнения

Приведем задачу, которая заключается не только в нахождении дискриминанта, но и в решении уравнения. Необходимо найти корни для равенства -2*x²+7-9*x = 0.

В этом примере дискриминант равен следующему значению: D = 81-4*(-2)*7= 137. Тогда корни уравнения определятся так: x = (9±√137)/(-4). Это точные значения корней, если вычислить приближенно корень, тогда получатся числа: x = -5,176 и x = 0,676.

Геометрическая задача

Решим задачу, которая потребует не только умения вычислять дискриминант, но и применения навыков абстрактного мышления и знания, как составлять квадратные уравнения.

У Боба было пуховое одеяло размером 5 x 4 метра. Мальчик захотел пришить к нему по всему периметру сплошную полосу из красивой ткани. Какой толщины будет эта полоса, если известно, что у Боба имеется 10 м² ткани.

Пусть полоса будет иметь толщину x м, тогда площадь ткани по длинной стороне одеяла составит (5+2*x)*x, а поскольку длинных сторон 2, то имеем: 2*x*(5+2*x). По короткой стороне площадь пришитой ткани составит 4*x, так как этих сторон 2, то получаем значение 8*x. Отметим, что к длинной стороне было добавлено значение 2*x, поскольку длина одеяла увеличилась на это число. Общая пришитая к одеялу площадь ткани равна 10 м². Поэтому получаем равенство: 2*x*(5+2*x) + 8*x = 10 => 4*x²+18*x-10 = 0.

Для этого примера дискриминант равен: D = 18²-4*4*(-10) = 484. Его корень равен 22. Воспользовавшись формулой, находим искомые корни: x = (-18±22)/(2*4) = (-5; 0,5). Очевидно, что из двух корней подходит по условию задачи только число 0,5.

Таким образом, полоса из ткани, которую пришьет Боб к своему одеялу, будет иметь ширину 50 см.