Взаимное расположение плоскостей: необходимые сведения

Плоскостью называется двумерный геометрический объект. Он является составной частью всех многогранников. Рассмотрим в статье с математической точки зрения различные варианты взаимного расположения плоскостей в пространстве.

Что называют плоскостью?

Каждый человек знаком с этим понятием, поскольку при решении бытовых задач он часто сталкивается с ним. Так, говорят о плоскости стены, доски, металлического листа и так далее. В математике под этим термином понимают такой объект, который удовлетворяет следующим признакам:

• Он состоит из бесконечного числа точек.
• Если соединить каждую точку поочередно со всеми остальными, то получится бесконечный набор векторов, причем все они будут перпендикулярны некоторому одному вектору. Последний называется нормалью к плоскости.

Пример плоскости в трехмерном пространстве приведен ниже на рисунке.

Уравнения плоскости

Прежде чем отвечать на вопрос, каково взаимное расположение плоскостей, необходимо привести математические выражения, задающие рассматриваемый геометрический объект. Начнем с общего уравнения, которое может быть представлено в следующей форме:

A*x + B*y + C*z + D = 0.

Большие латинские буквы здесь являют собой простые числа. Маленькие буквы - это совокупность координат всех точек, которые удовлетворяют данному уравнению (лежащие в плоскости точки).

Приведенное выражение удобно использовать для решения многих геометрических задач, поскольку в нем содержится информация о нормальном векторе n¯. Координатами n¯ являются числа A, B и C.

Следующим уравнением плоскости, которое применяют для решения задач, является векторное. Оно выглядит следующим образом:

(x, y, z) = (x₀, y₀, z₀) + α*(a₁, b₁, c₁) + β*(a₂, b₂, c₂).

Приведенное выражение выглядит несколько громоздким, однако в нем нет ничего сложного. Первое слагаемое в правой части равенства - это координаты точки, лежащей в плоскости, два последующих слагаемых - это координаты лежащих в плоскости векторов. Параметры α и β являются независимыми и принимают произвольные значения.

Векторное уравнение удобно применять, если необходимо получить параметрическое выражение для плоскости. Кроме того, несложно вычислить координаты нормали к плоскости. Для этого следует умножить векторно два заданных вектора.

Наконец, еще одним важным видом уравнения плоскости является так называемое выражение в отрезках. Оно выглядит так:

x/p + y/q + z/l = 1.

Здесь стоящие в знаменателях латинские буквы p, q и l представляют собой числа, являющиеся отрезками, которые отсекает плоскость при пересечении прямоугольных осей координат. Откуда и соответствующее название этого вида уравнения. Очевидно, что его удобно применять, если необходимо изобразить графически объект.

Несложно показать, что все виды записанных уравнений преобразуются друг в друга.

Взаимное расположение плоскостей

Плоскость - это двумерный объект. В трехмерном пространстве существует всего два принципиально отличающихся способа взаимного расположения двух плоскостей:

• они параллельны друг к другу;
• они пересекаются.

Действительно, если плоскости не имеют общих точек, значит, они никогда не пересекаются, то есть являются параллельными. Наоборот, если рассматриваемые объекты имеют хотя бы одну общую точку, значит, они пересекаются. Отметим, что геометрическим объектом, образующимся в результате пересечения плоскостей, всегда является прямая линия.

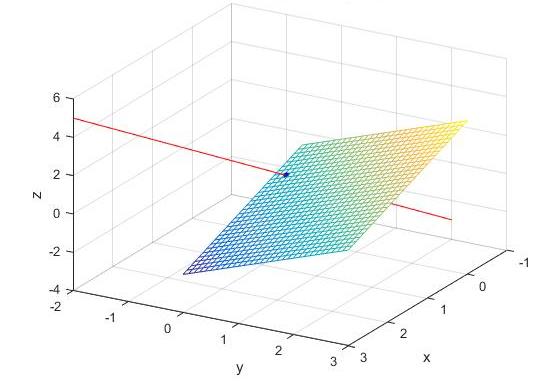
Параллельные плоскости

Теперь рассмотрим подробнее каждый из названных выше случаев. Предположим, что в общей форме заданы следующие две плоскости:

A₁*x + B₁*y + C₁*z + D₁ = 0;

A₂*x + B₂*y + C₂*z + D₂ = 0.

Как понять, являются ли они параллельными? Сделать это очень просто. Достаточно вспомнить о нормальных векторах. Если две плоскости параллельны между собой, значит, их нормали также параллельны. Выпишем координаты нормальных векторов к указанным плоскостям. Имеем:

n₁¯ = (A₁, B₁, C₁);

n₂¯ = (A₂, B₂, C₂).

Достаточным условием параллельности n₁¯ и n₂¯ является возможность задания одного из них через другой. Математически это записывается так:

n₁¯ = k*n₂¯.

Где k - некоторое (в том числе отрицательное) число. Если одну нормаль невозможно выразить путем умножения координат другой на число, то такие плоскости не будут параллельными.

Частным случаем параллельности плоскостей является их полное совпадение друг с другом. Тогда должны выполняться такие условия:

n₁¯ = k*n₂¯ и D₁ = k*D₂.

Пример параллельных плоскостей в пространстве приведен ниже.

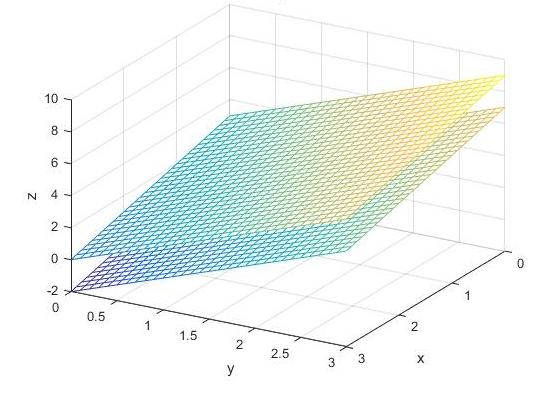
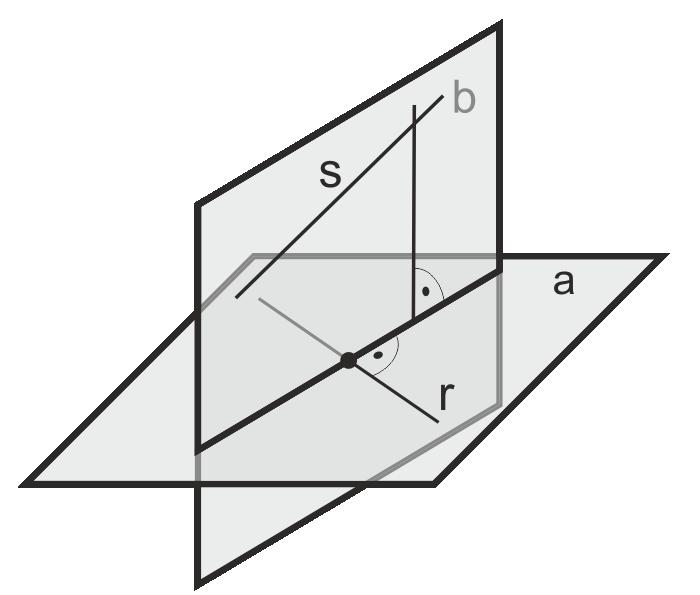
Пересекающиеся плоскости и угол между ними

Поскольку существует всего два варианта взаимного расположения плоскостей, то достаточно проверить, являются ли они параллельными или нет. В случае их пересечения часто возникает необходимость в определении соответствующего угла. Согласно определению, углом между рассматриваемыми геометрическими объектами является угол между их нормалями.

Таким образом, изучая вопрос взаимного расположения плоскостей и угла между плоскостями, достаточно рассчитать скалярное произведение векторов n₁¯ и n₂¯. Соответствующая формула примет вид:

θ = arccos(|(n₁¯*n₂¯)|/(|n₁¯|*|n₂¯|)).

Угол между плоскостями θ всегда является острым, поскольку в числителе стоит модуль скалярного произведения.

Следует отметить частный случай, когда две плоскости пересекаются под углом 90^o. Тогда достаточно вычислить скалярное произведение нормальных векторов. Оно будет равным нулю.

Прямая и плоскость

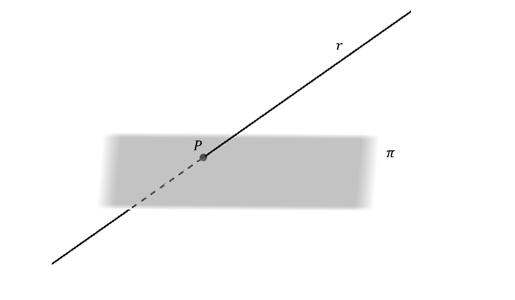
Кратко остановимся на вопросе взаимного расположения прямой и плоскости в пространстве. В трехмерной системе координат удобнее всего задавать плоскость в векторной форме. Она имеет вид:

(x, y, z) = (x₀, y₀, z₀) + λ*(a, b, c).

Здесь вектор (a, b, c) называется направляющим для прямой. Далее будем обозначать его u¯.

Существует три способа относительного расположения рассматриваемых геометрических объектов:

• Они параллельны. Для этого скалярное произведение u¯ и нормали n¯ плоскости должно быть равно нулю. И ни одна точка прямой не должна принадлежать плоскости.
• Прямая лежит в плоскости. Скалярное произведение u¯ и n¯ также равно нулю. И все точки прямой лежат в плоскости.
• Они пересекаются. В этом случае существует единственное число λ, удовлетворяющее системе уравнений плоскости и прямой. Если прямая пересекает плоскость под прямым углом, тогда ее направляющий вектор может быть выражен путем умножения на некоторое число вектора нормали.

Пример задачи

Закрепим полученные знания на примере решения следующей задачи. Заданы две плоскости следующими уравнениями:

2*x - y + 4 = 0;

(x, y, z) = (0, 1 , 1 ) + α*(0 , 1, 1 ) + β*(2 , 0 , 1 ).

Определите взаимное расположение плоскостей.

Нормальный вектор для первой известен. Он имеет следующие координаты:

n₁¯ = (2, -1, 0).

Чтобы определить вектор n₂¯, следует найти произведение лежащих в этой плоскости векторов. Имеем:

n₂¯ = [(0, 1, 1)*(2, 0, 1)] = (1, 2, -2).

Видно, что вектор n₂¯ не может быть получен из вектора n₁¯ путем умножения на число. Этот факт говорит о том, что рассматриваемые плоскости пересекаются. Угол пересечения можно рассчитать по приведенной выше формуле. Получаем:

(n₁¯*n₂¯) = ((2, -1, 0)*(1, 2, -2)) = (2 - 2 + 0 = 0.

Поскольку скалярное произведение равно нулю, значит, плоскости пересекаются под прямым углом.