Длина дуги: общая формула и особенности расчета

Дуга окружности - удивительный геометрический объект, скрывающий в себе множество загадок. А загадкой является в том числе вопрос о том, как найти длину этого криволинейного отрезка. В нашей статье мы не только дадим ответ на этот вопрос, но и рассмотрим разные методы вычисления, сравним их, выявим достоинства и недостатки. Также узнаем, где на практике можно столкнуться с необходимостью знания длины дуги окружности и как это знание применить с максимальной пользой. Погружаемся в увлекательный мир геометрии!

Основные понятия и определения

Для начала давайте разберемся в том, что же из себя представляет дуга окружности. Формальное определение звучит так: дугой окружности называется часть окружности, ограниченная двумя точками на ней.

То есть если мы возьмем произвольную окружность и отметим на ней две разные точки А и В, то отрезок окружности между ними и будет дугой АВ (рис. 1).

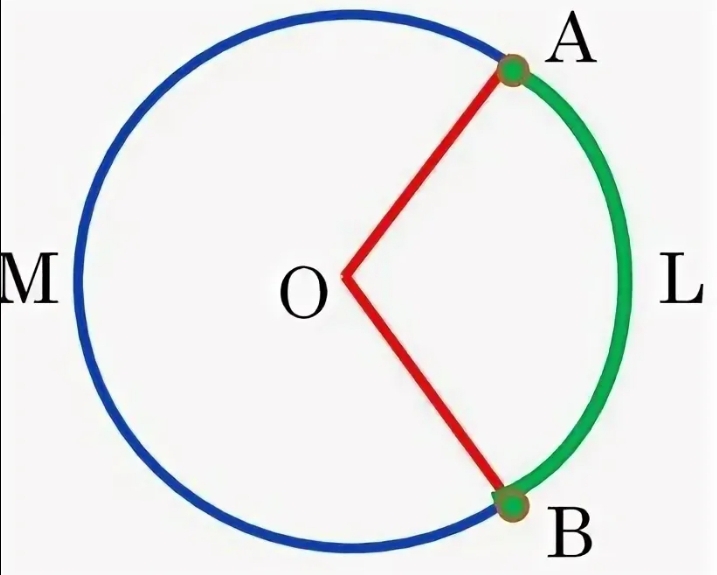
Рисунок 1. Дуга окружности

Через центр O окружности, к которой принадлежит дуга, можно провести два радиуса OA и OB и построить центральный угол AOB, опирающийся на дугу АВ. Этот угол также характеризует дугу.

Очевидно, что длина дуги АВ является важной геометрической величиной, которую необходимо как-то описать количественно, чтобы использовать на практике.

Общая формула длины дуги окружности

Как найти эту самую длину дуги АВ? Оказывается, существует несколько разных подходов. Рассмотрим самый распространенный и универсальный.

Поскольку дуга АВ является частью окружности, ее длина L должна быть пропорциональна длине всей окружности C. С другой стороны, центральный угол AOB, определяющий дугу АВ, тоже должен как-то соотноситься с полным углом окружности, равным 360° или 2π радиан.

Отсюда получаем формулу:

где:

• R - радиус окружности
• α - центральный угол в радианах

По данным формулам можно найти, как длину дуги окружности, так и длину самой окружности.