Что такое напряженность электрического поля

Напряженность электрического поля может иметь значительную важность при использовании конденсаторов, а также иных деталей для схем. Почему так? Давайте рассмотрим данное понятие с точки зрения физики.

Зачем было введено само понятие напряженности электрического поля

Оно характеризирует особый вид материи, которая существует около любого электрического заряда и проявляет себя во влиянии на другие подобные частицы. Напряженность – это характеристика данного поля. Принимать во внимание данное понятие необходимо из-за того, что существует влияние на электронные компоненты любой схемы, которая есть в любой электротехнике. А при игнорировании этого аспекта машины, в которых они есть, будут очень быстро выходить из строя, возможно даже, что мгновенно – при первом же запуске. Как напряженность электрического поля рассматривается современной наукой?

Что такое напряженность с точки зрения физики

Данному понятию было уделено много внимания – ещё бы, ведь от понимания данных процессов сейчас очень сильно зависит мощь нашей цивилизации. Под ней понимают векторную величину, которую используют, чтобы охарактеризовать электрическое поле в одной точке. Она численно равняется отношению силы, что воздействует на недвижимый точечный заряд, который рассматривается, к его величине:

Н=С/ВЗ, где:

1. Н – напряженность.
2. С – сила.
3. ВЗ – величина заряда, что рассматривается.

Вот как определить напряженность электрического поля. И вот почему её могут иногда называть его же силовой характеристикой. Что же выступает единственным отличием? От вектора силы, который действует на заряженную частицу, данный случай отличается наличием постоянного множителя. А что можно сказать про его величину?

Значение вектора в каждой точке пространства

Необходимо учитывать, что данная величина меняется вместе с изменением координат. Формально все точки векторного объема можно выразить такой записью: Е = Е (х, у, z, t). Она представляет напряженность электрического поля в виде функции пространственных координат. А теперь на них необходимо наложить векторы магнитной индукции. В результате можно получить электромагнитное поле, которое вместе со своими законами будет представлять предмет электродинамики. В чем измеряется напряженность данного объекта? Для этого используют показатель вольт на метр или ньютон на кулон (запись соответственно В/м или Н/Кл).

Напряжённость электрического поля в классической электродинамике

Она признана одной из основных фундаментальных величин. Сопоставимыми по важности можно назвать вектор магнитной индукции и электрический заряд. В некоторых случаях подобную значительность могут приобретать потенциалы электромагнитного поля. Более того, если соединить их вместе, то можно получить значение, которое покажет возможность влияния на другие объекты. Оно называется электромагнитным потенциалом. Существуют и другие понятия. Электрический ток, его плотность, вектор поляризации, напряженность магнитного поля – все они достаточно значимые и важные, но считаются только вспомогательными величинами. Давайте устроим краткий обзор основных контекстов, которые имеются в классической электродинамике относительно напряженности электрического поля.

Сила действия на заряженные частицы

Для выражения общего показателя воздействия магнитного поля использую формулу Лоренца:

С = ЭЗЧ*ВС+ЭЗЧ*Ск*^ВМИ.

С – сила воздействия магнитного поля на заряженную частицу.

ЭЗЧ – электрический заряд одной частицы.

ВМИ – вектор магнитной индукции.

Ск – скорость движения частицы.

*^ - векторное произведение.

Если разобраться в формуле, то можно увидеть, что она полностью согласуется с ранее данным определением, чем является напряженность электрического поля. Но само уравнение обобщено, поскольку в него включено действие на заряженную частицу со стороны магнитного поля при движении оной. Также предполагается, что объект рассмотрения является точечным. Формула позволяет рассчитывать силы, которыми действует электромагнитное поле на тело любой формы, в котором произвольное распределение зарядов и токов. Необходимо только разбить сложный объект на маленькие части, каждая из них может считаться точкой, и тогда к ней становится возможным применение формулы.

Что можно сказать про остальные подсчёты

Другие уравнения, которые применяются при расчетё электромагнитных сил, считают следствиями формулы Лоренца. Также их называют частными случаями её применения. Хотя для практического применения даже в самых простых задачах всё же необходимо иметь ещё небольшой багаж знаний, о которых сейчас и будет рассказано.

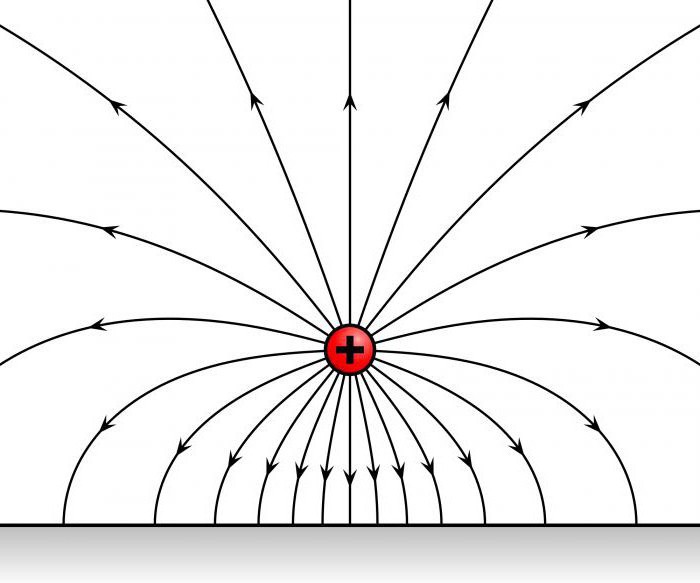
Электростатика

Занимается частными случаями, когда заряженные тела являются неподвижными, или их скорость передвижения настолько мала, что их таковыми считают. Как же посчитать напряженность электрического поля в данном случае? В этом нам поможет скалярный потенциал:

НЭП = -∆СП.

НЭП – напряженность электрического поля.

СП – скалярный потенциал.

Верно и обратное. Полученное значение называется электростатическим потенциалом. Также подобный подход упрощает уравнение Максвелла, и оно превращается в формуле Пуассона. Для частного случая областей, которые свободны от заряженных частиц, используют подсчёты по методу Лапласа. Обратите внимание – все уравнения линейные, а соответственно, к ним применяется принцип суперпозиции. Для этого следует найти поле только одного точечного единичного заряда. Затем следует обсчитать напряженность или потенциал поля, что создаются их распределением. Знаете, как называют полученный результат? Наверняка нет. А имя ему - напряженность электрического поля точечного заряда.

Уравнения Максвелла

Они вместе с формулой силы Лоренца составляют теоретический фундамент классической электродинамики. Традиционная форма представлена. Поскольку описывать каждое из них – это долго, то мною они будут представлены в виде картинки. Считается, что этих четырёх уравнений и формулы силы Лоренца достаточно, чтобы полностью описать классическую (только её, а не квантовую) электродинамику. Но что делать с практикой? Для решения реальных задач может потребоваться ещё уравнение, которое описывает движение материальных частиц (в классической механике в их роли выступают законы Ньютона). Также будет нужной информация о конкретных свойствах сред и физических тел, которые рассматриваются (их упругость, электропроводность, поляризация и подобное). Для решения задач могут применяться и другие силы, что не входят в рамки электродинамики (как то гравитация), но которые бывают нужными, чтобы построить замкнутую систему уравнений или решить конкретную проблему.

Заключение

Что же, подводя итог, можно сказать, что напряженность электрического поля была рассмотрена довольно полно, как в целом, так и некоторые частные случаи. Данных, представленных в рамках статьи, должно с лихвой хватить, чтобы рассчитывать параметры для своих будущих конструкций. Про графическое изображение можно сказать, что векторы напряженности электрического поля изображаются с помощью силовых линий, которые считаются касательными к каждой точке. Этот способ описания впервые был введён Фарадеем. На этом про напряженность электрического поля автор заканчивает и благодарит вас за уделенное внимание.