Неинерциальная система отсчета: определение, примеры

Все системы отсчёта делят на инерциальные и неинерциальные. Инерциальная система отсчёта лежит в основе механики Ньютона. Она характеризует равномерное прямолинейное движение и состояние покоя. Неинерциальная система отсчёта связана с ускоренным движением по разной траектории. Это движение определяется по отношению к инерциальным системам отсчёта. Неинерциальная система отсчёта связана с такими эффектами, как сила инерции, центробежная и сила Кориолиса.

Все эти процессы возникают в результате движения, а не взаимодействия между телами. Законы Ньютона в неинерциальных системах отсчёта зачастую не работают. В таких случаях к классическим законам механики добавляются поправки. Силы, обусловленные неинерциальным движением, учитываются при разработке технических изделий и механизмов, в том числе тех, где присутствует вращение. В жизни мы сталкиваемся с ними, перемещаясь в лифте, катаясь на карусели, наблюдая за погодой и течением рек. Их учитывают и при расчёте движения космических аппаратов.

Инерциальные и неинерциальные системы отсчёта

Для описания движения тел инерциальные системы отсчёта подходят не всегда. В физике выделяют 2 вида систем отсчёта: инерциальные и неинерциальные системы отсчёта. Согласно механике Ньютона, любое тело может быть в состоянии покоя либо равномерного и прямолинейного движения, за исключением случаев, когда на тело оказывается внешнее воздействие. Такое равномерное движение называют движением по инерции.

Инерциальное движение (инерциальные системы отсчёта) составляет основу механики Ньютона и трудов Галилея. Если считать звёзды неподвижными объектами (что на самом деле не совсем так), то любые объекты, движущиеся относительно них равномерно и прямолинейно, будут образовывать инерциальные системы отсчёта.

В отличие от инерциальных систем отсчёта, неинерциальная система перемещается по отношению к указанной с определенным ускорением. При этом использование законов Ньютона требует дополнительных переменных, в противном случае они будут неадекватно описывать систему. Что бы ответить на вопрос, какие системы отсчёта называются неинерциальными, стоит рассмотреть пример неинерциального движения. Таким движением является вращение нашей и других планет.

Движение в неинерциальных системах отсчёта

Коперник первым показал, насколько сложным может быть движение, если в нём участвует несколько сил. До него считалось, что Земля движется сама по себе, в соответствии с законами Ньютона, и потому ее движение является инерциальным. Однако Коперник доказал, что Земля обращается вокруг Солнца, то есть совершает ускоренное движение по отношению к условно неподвижному объекту, каковым может являться звезда.

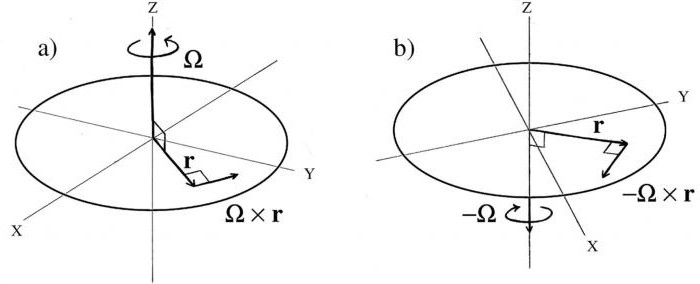
Итак, есть разные системы отсчёта. Неинерциальными называют только те, где есть ускоренное движение, которое определяется по отношению к инерциальной системе.

Земля как система отсчёта

Неинерциальная система отсчёта, примеры существования которой можно встретить практически везде, типична для тел со сложной траекторией движения. Земля вращается вокруг Солнца, что создаёт ускоренное движение, характерное для неинерциальных систем отсчёта. Однако в повседневной практике всё, с чем мы сталкиваемся на Земле, вполне согласуется с постулатами Ньютона. Всё дело в том, что поправки на неинерциальное движение для связанных с Землёй систем отсчёта, очень незначительны и большой роли для нас не играют. И уравнения Ньютона по этой же причине оказываются в целом справедливы.

Маятник Фуко

Впрочем, в некоторых случаях без поправок не обойтись. Например, известный во всём мире маятник Фуко в соборе Санкт-Петербурга совершает не только линейные колебания, но ещё и медленно поворачивается. Этот поворот обусловлен неинерциальностью движения Земли в космическом пространстве.

Впервые об этом стало известно в 1851 году после опытов французского ученого Л. Фуко. Сам эксперимент проводился не в Петербурге, а в Париже, в огромном по размерам зале. Вес шара маятника был около 30 кг, а протяжённость соединительной нити – целых 67 метров.

В тех случаях, когда для описания движения недостаточно только формул Ньютона для инерциальной системы отсчёта, в них добавляют так называемые силы инерции.

Свойства неинерциальной системы отсчёта

Неинерциальная система отсчёта совершает различные движения относительно инерциальной. Это может быть поступательное движение, вращение, сложные комбинированные движения. В литературе приводится и такой простейший пример неинерциальной системы отсчёта, как ускоренно движущийся лифт. Именно из-за его ускоренного движения мы чувствуем, как нас придавливает к полу, или, наоборот, возникает ощущение, близкое к невесомости. Законы механики Ньютона такое явление объяснить не могут. Если следовать знаменитому физику, то в любой момент на человека в лифте будет действовать одна и та же сила тяжести, а значит и ощущения должны быть одинаковы, однако, в реальности всё обстоит иначе. Поэтому к законам Ньютона необходимо добавить дополнительную силу, которая и называется силой инерции.

Сила инерции

Сила инерции является реальной действующей силой, хотя и отличается по природе от сил, связанных с взаимодействием между телами в пространстве. Она учитывается при разработке технических конструкций и аппаратов, и играет важную роль в их работе. Силы инерции измеряются различными способами, например, при помощи пружинного динамометра. Неинерциальные системы отсчёта не являются замкнутыми, поскольку силы инерции считаются внешними. Силы инерции являются объективными физическими факторами и не зависят от воли и мнения наблюдателя.

Инерциальные и неинерциальные системы отсчёта, примеры проявления которых можно найти в учебниках физики – это действие силы инерции, центробежная сила, сила Кориолиса, передача импульса от одного тела к другому и другие.

Движение в лифте

Неинерциальные системы отсчёта, силы инерции хорошо проявляют себя при ускоренном подъёме или спуске. Если лифт с ускорением движется вверх, то возникающая сила инерции стремится прижать человека к полу, а при торможении тело, наоборот, начинает казаться более лёгким. По проявлениям сила инерции в данном случае похожа на силу тяжести, но она имеет совсем другую природу. Сила тяжести – это гравитация, которая связана с взаимодействием между телами.

Центробежные силы

Силы в неинерциальных системах отсчёта могут быть и центробежными. Вводить такую силу необходимо по той же причине, что и силу инерции. Яркий пример действия центробежных сил – вращение на карусели. Тогда как кресло стремится удержать человека на своей «орбите», сила инерции приводит к тому, что тело прижимается к внешней спинке кресла. Это противоборство и выражается в появлении такого явления, как центробежная сила.

Сила Кориолиса

Действие этой силы хорошо известно на примере вращения Земли. Назвать её силой можно лишь условно, поскольку таковой она не является. Суть её действия состоит в том, что при вращении (например, Земли) каждая точка сферического тела движется по окружности, тогда как объекты, оторванные от Земли, в идеале перемещаются прямолинейно (как, например, свободно летящее в космосе тело). Поскольку линия широты является траекторией вращения точек земной поверхности, и имеет вид кольца, то любые тела, оторванные от нее и первоначально движущиеся вдоль этой линии, перемещаясь линейно, начинают всё больше отклоняться от неё в направлении более низких широт.

Другой вариант – когда тело запущено в меридиональном направлении, но из-за вращения Земли, с точки зрения земного наблюдателя, движение тела уже не будет строго меридиональным.

Сила Кориолиса оказывает большое влияние на развитие атмосферных процессов. Под её же влиянием вода сильнее ударяет в восточный берег текущих в меридиональном направлении рек, постепенно размывая его, что приводит к появлению обрывов. На западном же, напротив, откладываются осадки, поэтому он более пологий и часто заливается водой при паводках. Правда, это не единственная причина, приводящая к тому, что один берег реки выше другого, но во многих случаях она является доминирующей.

Сила Кориолиса имеет и экспериментальное подтверждение. Оно было получено немецким физиком Ф. Райхом. В эксперименте тела падали с высоты 158 м. Всего было проведено 106 таких опытов. При падении тела отклонялись от прямолинейной (с точки зрения земного наблюдателя) траектории приблизительно на 30 мм.

Инерциальные системы отсчёта и теория относительности

Специальная теория относительности Эйнштейна создавалась применительно к инерциальным системам отсчёта. Так называемые релятивистские эффекты, согласно этой теории, должны возникать в случае очень больших скоростей движения тела относительно «неподвижного» наблюдателя. Все формулы специальной теории относительности также расписаны для равномерного движения, свойственного инерциальной системе отсчёта. Первый постулат этой теории утверждает равноценность любых инерциальных систем отсчёта, т. е. постулируется отсутствие особых, выделенных систем.

Однако это ставит под сомнение возможность проверки релятивистских эффектов (как и сам факт их наличия), что привело к появлению таких явлений, как парадокс близнецов. Поскольку системы отсчёта, связанные с ракетой и Землёй, принципиально равноправны, то и эффекты замедления времени в паре "Земля – ракета" будут зависеть только от того, где находится наблюдатель. Так, для наблюдателя на ракете, время на Земле должно идти медленнее, а для человека, находящегося на нашей планете, наоборот, оно должно идти медленнее на ракете. В результате близнец, оставшийся на Земле, увидит своего прибывшего брата более молодым, а тот, кто был в ракете, прилетев, должен увидеть моложе того, кто остался на Земле. Понятно, что физически такое невозможно.

Значит, чтобы наблюдать релятивистские эффекты, нужна какая-то особая, выделенная система отсчёта. Например, предполагается, что мы наблюдаем релятивистское увеличение времени жизни мюонов, если они движутся с околосветовой скоростью относительно Земли. Это значит, что Земля должна (причём, безальтернативно) обладать свойствами приоритетной, базовой системы отсчёта, что противоречит первому постулату СТО. Приоритет возможен только в случае, если Земля является центром вселенной, что согласуется только с первобытной картиной мира и противоречит физике.

Неинерциальные системы отсчёта как неудачный способ объяснения парадокса близнецов

Попытки объяснить приоритет "земной" системы отсчёта не выдерживают никакой критики. Некоторые ученые такой приоритет связывают именно с фактором инерциальности одной и неинерциальности другой системы отсчёта. При этом систему отсчёта, связанную с наблюдателем на Земле, считают инерциальной, при том, что в физической науке она официально признана неинерциальной (Детлаф, Яворский, курс физики, 2000). Это первое. Второе - это всё тот же принцип равноправия любых систем отсчёта. Так, если космический корабль уходит от Земли с ускорением, то с точки зрения наблюдателя на самом корабле, он статичен, а Земля, напротив, улетает от него с возрастающей скоростью.

Получается, что сама Земля является особой системой отсчёта либо наблюдаемые эффекты имеют иное (не релятивистское) объяснение. Может быть, процессы связаны с особенностями постановки или интерпретации экспериментов, либо с иными физическими механизмами наблюдаемых явлений.

Заключение

Таким образом, неинерциальные системы отсчёта приводят к появлению сил, которые не нашли своего места в законах механики Ньютона. При расчётах для неинерциальных систем учёт этих сил является обязательным, в том числе, при разработке технических изделий.