Как узнать площадь равностороннего треугольника: основные формулы
Найти площадь равностороннего треугольника можно по любой формуле для произвольной фигуры данного типа или воспользоваться теми, в которых уже учтена особенность именно этой фигуры и математические выражения существенно упрощены.
Первый случай только требует замены всех сторон одинаковым значением и учета того, что все углы у треугольника равны 60º. Потом останется провести несложные преобразования, которые и приведут к формулам, данным в готовом виде немного ниже.
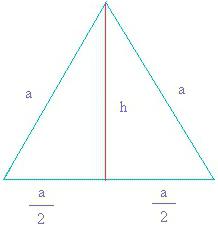
Формула 1: известна сторона
В этой и последующих формулах приняты стандартные обозначения величин треугольника. Подробнее их можно посмотреть в предложенной таблице.
| Величина | Ее обозначение |
| сторона | а |
| площадь | S |
| высота | н |
| радиусы окружностей вписанной и описанной | r и R, соответственно |
Расчет площади треугольника в этом случае будет осуществляться по формуле:
S = √3/4 * а2.
Она легко получается из той, которая известна для произвольной фигуры с тремя сторонами. Просто в формуле нужно учесть то, что все стороны у треугольника равны.
Если говорить более точно, то потребуется формула Герона: S = √(p(p-a)(p-b)(p-c)). Значение полупериметра для равностороннего треугольника будет равно 3а/2. Таким образом, в каждой скобке под корнем получится выражение ((3а/2) - а). Оно даст после преобразования а/2.
Так как скобок три, то у этого выражения появится третья степень. А значит, оно преобразится в а3/8.
Его еще нужно умножить на полупериметр, который определяется как сумма сторон, разделенная на 2. Получится выражение: 3а4/16. После извлечения квадратного корня как раз и останется то выражение, что дано в первой формуле для площади равностороннего треугольника.
Поэтому нет необходимости запоминать много формул. Можно просто запомнить одну — Герона. Из нее путем простых математических преобразований получаются все остальные, например, для равностороннего треугольника.
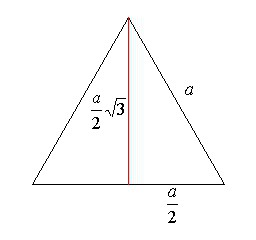
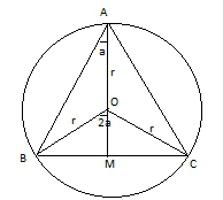
Формула 2: дан радиус вписанной окружности
Это выражение очень напоминает предыдущую запись. Но все же есть существенные отличия: используется другая буква, иррациональность ушла в знаменатель, появился множитель 3 и исчезла цифра 4. В общем, ее легко запомнить.
S = 3√3 * r2.
Эту формулу тоже легко получить из той, которая дана для произвольного треугольника. В ней радиус умножается на сумму сторон и делится на 4. Поскольку стороны имеют одинаковое значение, что сумма заменится на 3а. Теперь нужно убрать «а», чтобы осталось только значение радиуса. Для этого потребуется выражение, в котором сторона делится на произведение 2 и синуса противолежащего стороне угла. Так как угол равен 60º, то значение синуса будет √3/2. Тогда сторона выразится через радиус так: а = √3R. После несложного преобразования можно прийти к тому выражению для площади, которое дано вначале.
Формула 3: дана описанная окружность и ее радиус
Она очень похожа на первую. Только в ее числителе появляется цифра 3 и поменялась буква на R.
S = 3√3/4 * R2.
Поскольку радиус в два раза больше того, который рассматривался в предыдущем пункте, то понятно, как она получается. В ней просто вместо r ставится R/2. И проводятся необходимые преобразования.
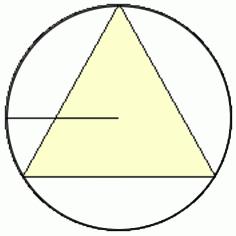
Поэтому формулу можно не запоминать. Только держать в памяти соотношение радиусов вписанной и описанной около равностороннего треугольника окружностей.
Формула 4: известна высота
В этом случае площадь равностороннего треугольника равна:
S = н2 / √3.
Чтобы понять, как получается такая формула, потребуется опять воспользоваться общей для всех треугольников. Она выглядит как произведение стороны на высоту и на ½. Теперь, чтобы узнать площадь равностороннего треугольника, придется вспомнить или вывести математическое выражение для высоты.
Ее несложно узнать, если воспользоваться тем фактом, что высота образует прямоугольный треугольник. Значит, высота может быть найдена как катет - из теоремы Пифагора. Второй катет будет равен половине стороны, так как высота является еще и медианой (это известное свойство равностороннего треугольника). Тогда высота будет определяться как квадратный корень из разности двух квадратов. Первый «а», а второй «а/2». После возведения во вторую степень и извлечения корня остается: н = (√3/2)*а. Из него а = 2н/√3. После подстановки его в основную для всех треугольников формулу получится то выражение, которое указано в начале раздела.
Пример №1
Условие. Вычислить площадь равностороннего треугольника, если известно, что его сторона имеет значение 4 см.
Решение. Поскольку известно значение сторон фигуры, то необходимо пользоваться первой формулой.
Сначала потребуется возвести в квадрат число 4. От этого действия получится число 16. Теперь оно сокращается с четверкой, стоящей в знаменателе. И в итоге в числителе остается 4 и √3, а знаменатель становится равным единице, значит, его можно просто не записывать. Это результат, который и требовалось найти в задаче.
Ответ: 4√3 см2.
Пример №2
Условие. Все стороны равностороннего треугольника равны 2√2 дм. Вычислить его площадь.
Решение. Рассуждения такие же, как в первой задаче. Только значение квадрата стороны будет другим. В нем нужно отдельно возвести во вторую степень 2 и иррациональность. И результат будет таким: 4*2 = 8. После сокращения со знаменателем остается 2 и √3 в числителе дроби, а знаменатель исчезает.
Ответ: 2√3 дм2.
Пример №3
Условие. В равносторонний треугольник вписана окружность, ее радиус 2,5 см. Необходимо вычислить площадь треугольника.
Решение. Для расчета искомой величины потребуется воспользоваться второй формулой.
Сначала значение радиуса нужно возвести в квадрат. Получится 6,25. Потом это значение требуется умножить на 3. Результатом этого действия станет число 18,75. Но это еще не конечное значение: в нем будет множитель √3, который присутствует в используемой формуле.
Ответ: 18,75√3 см2.
Пример №4
Условие. Требуется определить, чему равна площадь равностороннего треугольника, если известна его высота — 3 дм.
Решение. Естественно, что выбрать нужно четвертую формулу. С ее помощью проще всего найти ответ этой задачи.
Достаточно только возвести в квадрат число 3, то есть высоту, что даст значение 9. А потом разделить его на √3, стоящий в формуле.
Поскольку в математике не принято оставлять иррациональность в знаменателе ответа, то от нее нужно избавиться. Для этого дробь 9/√3 потребуется умножить на дробь с одинаковыми числителем и знаменателем, а именно √3/√3. От этого действия в числителе появится значение 9√3, а в знаменателе появится число 3.
Эту дробь можно и нужно сократить на 3. Это конечный результат.
Ответ: площадь — 3√3 дм2.
Пример №5
Условие. Дан равносторонний треугольник, площадь которого равна 27 см2. По этой величине нужно узнать длину стороны фигуры.
Решение. Поскольку речь идет о стороне, то подойдет первая формула. Из нее можно сразу вывести математическое выражение, которое позволит определить сторону треугольника.
Для этого площадь нужно умножить на 4 и разделить на квадратный корень из трех. Так получится значение для стороны в квадрате. Чтобы получить просто сторону, нужно извлечь корень. Выражение для стороны будет выглядеть так: а = 2 * √(S/√3).
Так как площадь известна, то можно сразу приступать к вычислениям. Подкоренное выражение выглядит как частное 27 и √3. Нужно избавиться от иррациональности в знаменателе. Получится 27√3, разделенное на 3. После сокращения в знаменателе остается 1, которую можно не писать, а в числителе остается 9√3.
Следующим действием будет извлечение корня из получившегося выражения. Первый множитель дает значение 3. А вот второй - √3 - требует к себе внимания. Чтобы упростить задачу, можно извлечь эти корни и округлить значения.
√3 = 1,73; теперь из него еще раз извлекаем корень и получаем 1,32.
Осталось только умножить его на 2 и получить искомый результат.
Ответ: сторона равна 2,64 см.
Похожие статьи
- Что такое периметр и его применение на практике
- Достопримечательности Москвы: Тишинская площадь
- Бумажный флексагон. Как сделать увлекательную головоломку?
- Аномальные свойства воды: причины, значение
- Созвездия северного полушария: названия, фото. Самое яркое созвездие северного полушария
- Как формулируется и доказывается теорема косинусов?
- Какие существуют запрещающие дорожные знаки? Запрещающие знаки: фото, описание и комментарии
