Энергия электрического поля: эксперименты и формулы

Когда рассматривается энергия электрического поля, следует изучать ее накопление и расходование. Накопителями энергии являются электроконденсаторы. При небольших габаритах такое устройство способно сосредотачивать в себе большое количество энергии.

При изучении конденсаторов становится легче понимать электростатические законы и возможности современных приборов. Таковыми являются, например, известные цифровые мультимеры, с помощью которых проводят измерения в пикофарадах. Сначала параметры следует оценивать, используя электростатические методы, а после этого — с применением мультимера.

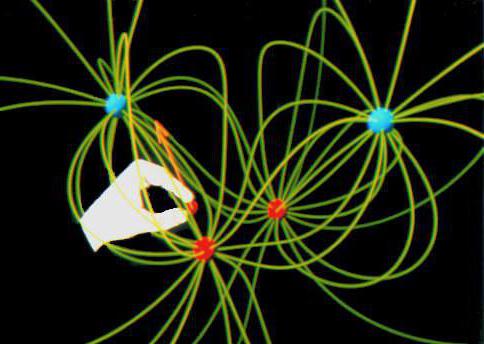
Электрическая емкость удлиненного проводника

Изучение этого устройства дает лучшее понимание в вопросе, что такое энергия электрического поля. Проводники способны накапливать и сохранять заряды. Это свойство называется электрической емкостью.

Для понимания зависимости потенциала удлиненного проводника от заряда необходимо измерить потенциалы заряженного тела. Удобно это сделать относительно земли.

Электрометр с полым проводящим шаром и заземленным корпусом используют в виде электростатического вольтметра и измеряют потенциал тела относительно земли.

Шариком-пробником касаются электрического источника, перенося таким образом внутрь него заряд. При этом вольтметр покажет наличие определенного потенциала.

Повторяя опыт можно прийти к выводу, что отношение заряда к потенциалу постоянно.

Поменяв полый шар на другой и проделав те же опыты, если вольтметр покажет большие значения по сравнению с предыдущими, можно сделпть вывод о меньшей емкости второго шарика.

В международной системе СИ единица измерения электрической емкости - фарад.

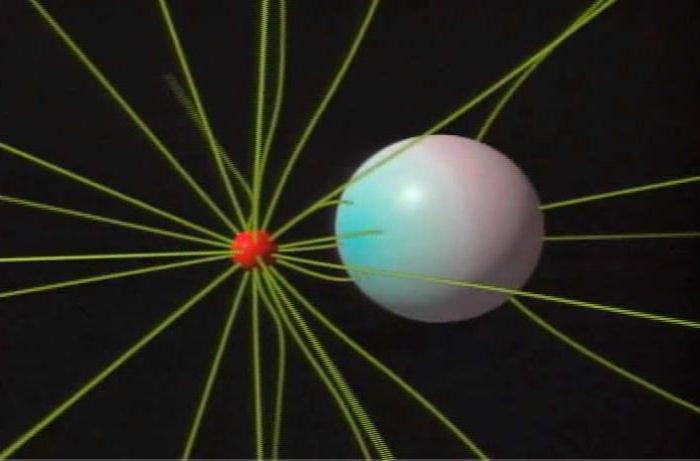
Опыт со сферическим проводником

Если в среде с диэлектрической проницаемостью взять сферический проводник, где потенциал в бесконечности равен нулю, то потенциал в сфере с зарядом будет равен Q/4ПƐ˳ƐR, а электрическая емкость C=4ПƐ˳ƐR,

Получается, что электрическая емкость удлиненного шара пропорциональна его радиусу.

Из опытов следует, что тела считаются удлиненными в случае, если окружающие тела не вызывают существенного перераспределения заряда в них.

Конденсатор

Из двух одинаковых параллельных пластин делают конденсатор и подсоединяют к нему электрометр, который будет работать в виде вольтметра. К его стержню подводят проводящую сферу. Пластину заряжают, перенося заряд с эбонитовой палочки. Тогда вольтметр покажет наличие напряжения, возникшего между пластинами.

Перенеся равные заряды внутрь полой сферы, увеличим показания прибора. Поэтому емкость у пластин будет следующей: C=q/U, способной работать в роли конденсатора, накапливающего заряд электричества (где q – это заряд одной из пластин).

Емкость плоского конденсатора

Емкость плоского конденсатор C=ε̥ε/d, где d – расстояние между пластинами.

Формула может быть подтверждена экспериментом. Собирается плоский конденсатор, заряжается и соединяются пластины с вольтметром. Не изменяя заряд, меняют другие показатели, наблюдая в это время за прибором. Показания будут обратно пропорциональны емкости: U=q/C–1/C.

Делая расстояние между пластинами больше, будем наблюдать увеличение напряжения. Смещая пластины параллельно и увеличивая площадь, получим сокращение напряжения, а емкость при этом увеличится. Если в промежуток между пластинами поместить диэлектрик, то показания вольтметра сократятся.

Так как в ходе эксперимента значение заряда не меняли, получается, что емкость конденсатора прямо пропорциональна перекрытию пластин и обратно пропорциональна d.

Параллельное и последовательное соединение конденсаторов

При параллельном соединении емкости приборов и их напряжения имеют одинаковые значения, а заряды — разное. Общий заряд равен их сумме по отдельности.

При последовательном соединении подключают вольтметр, имеющий полую сферу. Для одной обкладки первого конденсатора дается положительный заряд, тогда другая обкладка приобретет отрицательный, а при соединении с проводником второго прибора — положительный. Тогда оба конденсатора получат идентичные заряды, а напряжения у них будут иметь разные значения.

В результате емкость здесь будет определена по формуле: 1/C=1/C1+1/C2

Энергия плоского и произвольного конденсатора

На пластину подают заряд, имеющий значение, при котором разность потенциалов между пластинами стала равной U. Тогда напряженность будет равна E=U/d, где d – расстояние между объектами.

Одна из пластин находится в электрическом поле другой, где напряженность E/2. Тогда сила притяжения к другой пластине будет f=qE/2. Потенциальная энергия электрического поля заряда равна работе этого поля при сближении пластин.

Подставив ряд значений, получим, что энергия поля W=qU/2=q²/2C=CU²/2.

Такая формула подходит для любого конденсатора. Полная работа поля равна A=1/2qU.

То же самое получится, если применить удлиненный проводник вместо конденсатора.

Определение энергии экспериментальным путем

Замер энергии прибора производится по тепловому действию. В пробирку помещают спираль из металла, закрывают пробкой с трубкой, в которой имеется капелька воды. Получится газовый термометр. К спирали подключают конденсатор, а параллельно — электрометр с шаром, полым внутри.

Конденсатор заряжают при помощи шариков, а затем разряжают посредством спирали. Можно будет заметить перемещение капли в трубке.

После охлаждения воздуха и перемещения капли в начальное положение напряжение увеличивают. Капля переместится на несколько значений выше. Конденсатор меняют на большую емкость в два раза. Зарядив его до начального уровня, можно наблюдать перемещение, увеличенное вдвое.

Плотность энергии электрического поля

Задают энергию такую, чтобы конденсатор не имел значений, а принимались во внимание только величины, характеризующие поле. При этом должна быть вычислена энергия электрического поля на единицу объема.

В результате подстановок плотность энергии получается: ω=W/V=ε̥εΕ²/2, то есть она пропорциональна квадрату напряженности.

Энергия взаимодействия зарядов или энергия в электрическом поле

Итак, для зарядки конденсатора необходима работа, чтобы преодолеть силы электростатического притяжения между разными зарядами при их разделении. За счет этого возникнет запас потенциальной энергии.

Для зарядки любого тела также необходима работа, в данном случае для преодоления электростатического отталкивания между одноименными зарядами.

Взяв уединенный проводник, подаем заряд q. Потенциал поля на бесконечности будет равен нулю, а потенциал проводника - φ(q). Для перенесения малого заряда ∆q требуется работа:

∆A=φ(q)∆q.

Работа по зарядке уединенного проводника определяется по формуле:

A=W=1/2 φ(Q)Q=1/2C(φ(Q))²

На вопрос, где запасается энергия, отвечают двумя вариантами. По одному из них, это энергия взаимодействия зарядов на проводнике, а по другому, энергия — электрического поля получается, так как распределена в окружающем пространстве.

Какому ответу из этих двух отдать предпочтение — личное решение каждого ученика. Но, следует учесть, что при изучении переменных полей возможным становится только второй вариант, где энергия связывается с электрическим полем.